Toolkit "1vypolneno редица схеми на базата на учебник - учебник
ПРИЛОЖЕНИЕ 16 Януари
СПРАВКА 18
Toolkit "диаграми брой 1vypolneno базиран учебник AI Образцова, публикувана през 1953.
Това ръководство е предназначено да подпомогне студентите при изпълнението на графика на работа "диаграми №1» за курса "Дескриптивна геометрия".
Цел - да се научите как да се изгради линия на пресичане на определените равнинни фигури, за да се определи идентичността на съответните данни за прогнозите.
Графичен работа "диаграми №1» е първият независим заданието студент по темата "Дескриптивна геометрия". За извършване на тази работа, студентът трябва да проучи следните раздели на дескриптивна геометрия, "точки и линии", "самолет", "Взаимно положение на права линия и равнина", "Взаимното положение на двете равнини."
ОБЩА ИНФОРМАЦИЯ
Графичен работа "диаграми №1» се извършва в мащаб 1: 1 на формат А3 (297420 мм). В долния десен ъгъл на ученика A3 извършва основен надпис - формуляр 1, в съответствие с ГОСТ 2.104-68. Как се попълва заглавието блок е даден в приложение I. допълнителна графика 26 (1470 мм) се извършва в горния ляв ъгъл на формата. Примерно изпълнение на графичните произведения е даден в приложение I.
В съответствие с ГОСТ 2.303-68 задача се изпълнява следните видове линии:
- видими контурни линии на дебелина S, равни 0,60,8 mm;
- строителна линия - твърд тънък дебелина от до;
- скрити линии - дебелина бар от до;
- проследява помощни посреднически самолети изобразен отворени линии и дължина от 8-10 mm и дебелина до 1,5 S 2S.
МЕТОДИКА РЕШЕНИЯ диаграми
позоваване изпълнение включва три различни плосък геометрична фигура:
- № фигура 1 е даден координатите на три точки, фигура 2 № (многоъгълник) е напълно координатите на три точки, а останалите точки, в които един от координатите се заменя със състоянието на тяхната принадлежност към плоската № Фигура 2;
- фигура 3 се № стърчащата позиция (предна изпъкнала или хоризонтално проектиране) и е даден в схема форма на пръстен, сърповидно кръг или част от него.
Изпълнение на диаграмата се състои от графично разтвор на няколко проблема:
завърши липсва проекцията на многоъгълника;
изгради проекция линия на пресичане на триъгълника ABC и многоъгълник;
изгради линия на проекцията на пресичане: триъгълник с равнината на частното осигуряване; многоъгълник с равнината на частното осигуряване;
за определяне на видимостта на елементите в начертаните фигури, считайки непрозрачен фигура.
Входящи данни са дадени цифрови стойности на координатите и обобщени в Таблица 1 №.
Поред диаграми за изпълнение
За извършване на графичен работа студентът трябва да реши редица проблеми.
Задача 1. Изграждане на оригиналния чертеж на полигон (фиг. 1).
Хоризонталната проекция на ABCDE многоъгълник дефинирани напълно и изглед отпред на само три издатини на точки А V E . Необходимо е да се завърши предните прожекционни точки В. D. При изграждането на липсващата проекцията на полигона трябва да наблюдава състоянието на точки, принадлежащи към равнината на фигурата. За да отбележи C, D лежат в равнината, определена от три точки А, В и Е трябва да бъде, че те са по линиите, разположени в равнината. Тези линии са диагонални AC. АД и BE. хоризонтални издатини могат да изградят (фиг. 1а).
Фиг. 1. Изграждане на оригиналния полигон чертежа:
и - изграждането на липсващите проекциите на върховете; б - пропорционално разделяне на сегмента BE
Предната проекция петоъгълник извършва в диагонална проекция E . В равнината на петоъгълник са точки на пресичане на диагоналите на К и М хоризонтални проекции К и М са на разположение, и предната проекция получен чрез пресичане на линиите на прожекционни изготвени от К и М , с диагонал в E . Две точки са конструирани предна проекция на другите две диагоналите А и А K M , те трябва да лежи прожекционни точки В и Г , които се определят от техните хоризонтални проекции.
Ако линия съвпада с посоката на проекция връзка линия или стръмно наклонена към оста на координатната, липсва проекция точка е изработена от гледна точка пропорционално разделяне интервал: ако точката разделя сегмент в пропорционална част, проекцията на тази точка разделя проекцията на тази отсечка в същото съотношение , Фиг. 1Ь е необходимо за изграждане на хоризонтална проекция на точка М на. От проекция точка Б извършва линия под ъгъл по-малко от 90 до В E и оттам от проекция точка Б определят дължини равни по M и В E . Свързване Е и Е и успоредно на тази посока се извършва чрез M линия до неговото пресичане с B E . Вземете най-хоризонтална проекция M.
Задача 2: Изграждане на пресечната точка на MN в съответствие с равнината на триъгълника AB В.
Ако една права линия не е успоредна на равнината, тя пресича тази плоскост в реалната точка (вж. Фиг. 2).
Фиг. 2. Изграждане на пресечни точки с равнината
Алгоритъмът за решаване на проблема:
1) След предварително определено права линия MN изпълнява помощни равнина посреднически , перпендикулярни на равнината на челната издатина. Следователно, предната проекция равнина V всички точки на равнината операцията ще бъде очаква да права линия, съвпадаща с предната проекция линия М N .
2) Да се намери пресечната точка на референтната равнина посредник предварително определена равнина на триъгълника ABC. В рисунка линия (1,2).
3) Виж желаната точка на пресичане на линията на MN с равнината на триъгълника ABC. Тя се определя като пресечната точка на желаната линия с линията на пресичане на намерено референтната равнина, с посредничеството на триъгълник ABC равнина.
Определяне на видимостта на чертежа.
В описателен геометрия равнина се считат непрозрачен, така че е необходимо да се определи видимостта на прогнози.
За определяне на видимостта на чертежа с използване на метода на конкурентни точки, същността на която е да изберете двете кос линии.
За определяне на предната проекция самолет видимост V го направят. Изборът две кос линии в S и М N , предна издатини пресичат в точки 1 и 3. хоризонталната проекция определи, че проекцията на 3, който се намира на проекция линия М N , ще затвори точка проекция 1 лежи на проекцията на права линия в S , т.е.. за това ще бъде по-близо до наблюдателя. В чертежа, посока гледане наблюдател, показана със стрелка. Следователно, на предната равнина на проекция издатината ще М N Крайният проекция S . Видимостта в чужбина е проекция на точките на пресичане K.
За определяне на проекциите на хоризонталната равнина Н видимостта избират два кос линии А и S М N хоризонтални проекции пресичат в точки 4 и 5. За пред проекция определи, че проекцията на 5, лежи на правата линия М на проекция N , ще затвори точка проекция 4, лежи на линията А проекция S , т. К. Това ще бъде по-близо до наблюдателя. В чертежа, посока гледане наблюдател, показана със стрелка. Следователно, М N проекция върху хоризонтална равнина на проекция издатината ще затвори А S . Видимостта в чужбина е проекция на точките на пресичане K .
Задача 3. Изграждане на линията на пресичане на две равнини, едната от които заема особено място.
Като се има предвид две равнини: равнина ΔAVS - родово равнина ΔDEK равнина - частна равнина позиция, която е перпендикулярна на челната плоскост (Фигура 3.).
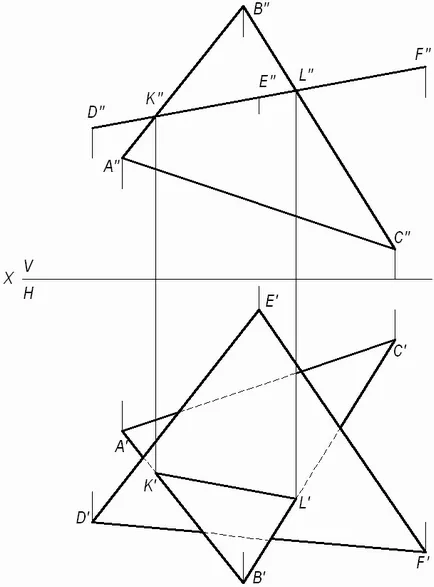
Фиг. 3. Конструкцията на линията на пресичане на две равнини, едната от които се
декларация за поверителност
Предна проекция ΔDEK съвпада с предна равнина на песен и предна проекция на линията на пресичане на триъгълници.
(KL) линия на пресичане на два триъгълника. Проекцията на тази линия на пресичане - фронталния и хоризонтална сградата въз основа на свойствата на К и Л точки, които да принадлежат към страни (AB) и (Британска Колумбия). съответно. Видимост триъгълници на хоризонталната проекция равнина определят чрез конкуриране точки дискутирани в Задача 2.
Задача 4. Изграждане на линията на пресичане на две равнини като цяло позиция.
Като се има предвид две родово равнина, определена от триъгълници ABC и DEK. Построяване на кръстовището на два триъгълника, за да се определи видимостта на триъгълници на прогнозите.
Права линия, получена от взаимното пресичане на две равнини, определени от две точки, всяка от които принадлежи на двете равнини едновременно. Общите точки са определени решения позиционни основните задачи на дескриптивна геометрия - изграждането на линията с равнината на пресечната точка (виж фигура 2 ..).
За да се реши този проблем със спомагателни самолета извършва на посредник лично положение (проектиране равнина). Решение на проблема е показана на фиг. 4.
Алгоритъмът за решаване на проблема:
1. Определяне на първата точка на линията на пресичане на два триъгълника - точка М.
1.1. Проектиране фронтална равнина, която преминава през DK страна на чертежа и предвид челен проследи V.
1.2. пресича равнината на триъгълник ABC равнина на правата линия (1,2) за изготвяне изгради две проекция на тази линия.
1.3. Директен (1,2) преминава по посока на точка М. DK изграждане на две прожекционни точки М и М .
2. Определяне на втората точка на желаната линия на пресичане на два триъгълника - точка Н.
2.1. Хоризонтално проектиране самолет проведено през страничната КБ и да зададете рисунка N хоризонтална следа.
2.2. DEK равнина пресича равнината на триъгълника на правата линия (3,4) за изготвяне изгради две проекция на тази линия.
2.3. Директен (3,4) преминава AB в точка Н. изгради две проекция точка N и N .
Самолет триъгълници ABC и DEK се пресичат в една права линия MN.
Фиг. 4. Изграждане на линията на пресичане на два триъгълника
3. Видимост плоски фигури върху проекциите определят от конкурентни точки.
За определяне на предната проекция равнина видимост V избере две кос линии D K и А B , предна издатини пресичат в точки 1 и 5. Хоризонталната проекция определи, че проекцията на 5, който се намира на проекция линия D K , ще затвори проекция точка 1, лежи на линията А проекция V , т. К. Това ще бъде по-близо до наблюдателя. Следователно, предната проекция равнина D K ще затвори проекцията А B . Видимост чужбина е проекция на линията на пресичане на М N .
За определяне на проекциите на хоризонталната равнина Н видимостта избират два кос линии А и D V E хоризонтални проекции пресичат в точки 3 и 6. За предната проекция ние определяме, че проекцията на 3, който се намира на проекция линия D E , ще закрие точка проекция 6, който се намира на проекция линия А B , тъй като тя ще бъде по-близо до наблюдателя. Следователно, проекцията върху хоризонтална равнина D затваря E проекция V . Видимост чужбина е проекция на линията на пресичане N M .
Задача 5. Изграждане две прожекционни линии на пресичане на равнина обща позиция, и следи от предварително определена равнина общата позиция, определена от успоредни прави линии с и Ь.
За да се реши този проблем спомагателната равнина се осъществява частен посредник позиция (ниво равнина) пресича предварително определена равнина в права, липсва издатина, която е лесно да се изгради и се пресичат в чертеж.
Графично решение на проблема е показано на фиг. 5.
Фиг. 5. Изграждане на линията на пресичане на две равнини
Спомагателни хоризонтална равнина, определена посредник у проследи γV и пресича равнината хоризонтално преминаваща през точка 3 и равнината хоризонтално (1, 2). Хоризонталната проекция на линиите на контура се пресичат в точка В. Изготвяне на предна проекция на точка К, като се използва имущество точки права линия. Точка К принадлежи на двете равнини и . Н. втора точка, обща за двете равнини и , равнината, определена от втори спомагателен посредник позиция частен делта (дефиниран в фигура следа δV). Предпочитан линия (RN) е пресечната точка на двете равнини и .
ПРИЛОЖЕНИЕ 1
СПРАВКА
Свързани документи:
Metodicheskoeposobie до заданието № 1 № 00. разгледаме С х д и м е дадено: а = 1.0 m, б = 1,5 m и с = 1.8 m, D = 1,2 т, р =. диаграми. диаграми образ, наречен също диаграми - заеми от френски (L'épure.
и управление в изграждането на образователна metodicheskoeposobie за провеждане на практически занятия по. посочване на общите резерви от време, както и схемата на ежедневните нужди на ресурса. Включено. Въз основа на тази схема се определя от максималната прием PE.
усукване, комплекс устойчивост, както и изграждането на диаграми само за плоски статично определими рамки. за разработването и публикуването на учебници и методически ръководства за училищата. Подходящи видове програми.
интензивност разпределен товар. Изграждане на диаграми на напречни сили и огъване. Все пак - за ефективност. Това ръководство за предавателно число w 1 / ω 2. Механизми за предаване на въртеливо движение ", изясняване насоки на темата и анализа.
Изчисляване на товароподемността на Насоки структури за населеното място и. дадени в справочници и учебници. например в [3]. За някои от тях. мащаб, наречен напречни сили Q диаграми и огъващите моменти M диаграми.