Структурата на електрическа верига

Структурните или топологични свойства включват вериги такива неговите характеристики, които не са свързани с характеристиките на съставните активни и пасивни елементи. Те включват следните понятия: клон възел верига.

клон верига част се нарича, чиито елементи са свързани последователно една след друга и се оптимизира чрез същия ток.

Възел верига нарича кръстовище на няколко клона. Възел свързва най-малко три клона и точка клон.

Клоните се считат за свързани последователно, ако те са оптимизирани от един и същ ток. Клоните се считат за свързани в паралел, ако те са свързани с една и съща двойка възли. По този начин, последователно свързване на елементите за тяхното общо параметър е текущата паралелно - напрежението между възли.

на схема контур електрически е набор от последователни разклонения. Възлите в които са свързани тези клонове, са точките на разклоняване. Когато пресичащо затворен контур начални и крайни точки съвпадат. В допълнително разбрано от затворен контур верига.

Верига, в която не разклонения се наричат ​​едно-, в присъствието на разклонения - многоканален. Множествена линия верига характеризира с броя на независими контури. Наборът от независими кръга се определя от факта, че всеки един от следващите бримки, като се започне от началното, се характеризира с най-малко един нов клон. Броят на независими вериги може да бъде определен от формула Ойлер:

където m - брой на клоновете,

п - брой на възли, където М> п пъти.

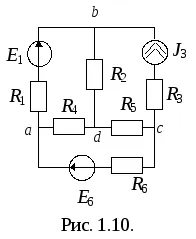
Схемата на фиг. 1.10. четири възли: А, В, С, D; Шест клона: аб, BD, ж.к., рекламни, окръг Колумбия, КС. по този начин броят на независимите пътища се определя от формула Ойлер, както следва:

Това може да включва следните схеми: ABCD, DBC, ADC или Абд, dbca, ADC и др.

закони Кирхоф

закони Кирхоф са в основата на теорията за линейни вериги и са също толкова закона на Ом, обобщение на експерименталните данни.

Izakon Kirchhoff (за токове). алгебрични сумата от течения в възел е равно на нула, или количеството на входящата и излизащата количество токове същото. Като правило, сумиране на постъпващия течения са взети от знака "+", и изтича - със знак "-".

IIzakon Кирхоф (за стрес): алгебричната сума от всички източници на ЕМП са срещнали при прекосяване на контура, равна на алгебричната сума от напреженията на всички потребители. В алгебрични форма

В обобщение със знак "+" включва EMF допринася източници (т.е. източници, които са в посока, съответстващо с байпас верига), и със знака "-" EMF противоположни източници. В сумиране напрежения потребителите със знака "+" се приема за всички потребители на напрежение, токовете от които са насочени в съответствие с байпас веригата, а знакът "-" напрежение се приема от всички други потребители. посока линия пакетът е избран произволно.

Превръщането на линейни пасивни електрически вериги

Еквивалентната част превръщане пасивна верига е заместител на веригата други пасивни, в които остават постоянни токове и напрежения останалата част от веригата не е подложен на трансформация. С прости трансформации включват подмяна на серия и паралелно свързан потребителите еквивалент на потребителя.

В серия връзка ролята на еквивалент устойчивост (резистентност или еквивалентен потребителя) играе сума от съпротивлението на всички потребители (фиг. 1.11.).

(1.10) От Закон II Кирхоф:

Когато две последователно свързани потребителите на:

Успоредно връзка ролята на еквивалент проводимост (или проводимост еквивалент потребителя) на играе сумата от проводимостта на всички потребители (фиг. 1.12.).

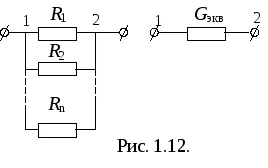
Това следва от закона аз Кирхоф:

Когато две паралелни връзки потребителите на:

По този начин, за изчисляване верига с серия потребителите целесъобразно да изразят свойства на стойности на съпротивлението, и свързани паралелно - стойностите на проводимостта.

Определяне на еквивалентната съпротивление в смесения съединението на потребителите се извършва чрез постепенно опростяване (нагъване) на оригиналната верига.

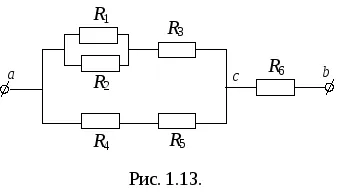
Серия връзка от R12 и R3:

Серия връзка на R4 и R5:

Паралелно свързване на R123 и R45.

Серия връзка RAC и R6:

По този начин, еквивалентно съпротивление

По-сложно е реципрочна превръщането на потребители, присъединени звезда или триъгълник. Такива трансформации трябва да се работи в тези случаи, когато връзката да е опростяване, не е възможно да се разпределят паралелен или сериен връзки потребителите.

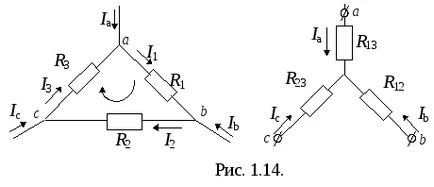
Възлите а. б. в и триъгълника. и звезда на фиг. 1.14. свързан с останалата част от веригата. Преобразуване на триъгълника в звездата трябва да бъде такова, че едни и същи стойности на потенциала на като триъгълник точки и звезди, вливащи се в тези точки, токовете са равни, а след това всички външни верига "няма да забележите" произведени замяна.

UAB изразят триъгълника през опциите на потребителите и тече на тези възли течения. Пишем уравнения на Кирхоф за схема и възли А и В.

Замяна в първото уравнение на I3 на токове и I2 в съответните изрази:

Според закона UAB напрежение на Ом за присъединяване на потребители триъгълник:

Сега ние получаваме израз за едно и също напрежение в звезда присъединяване на потребители:

За вериги данни равностойност на произволни стойности на токовете а и lb. е необходимо равенство на напрежения UAB за присъединяване на потребители делта и звезда. Това е възможно само при същите коефициенти на уравнения (1.15) и (1.16), т.е.

По същия начин, може да се получи експресия за определяне:

По този начин съпротивлението на звезда лъч е продукт на резистентност съседни страни на триъгълника, разделен на сумата от съпротивлението на триъгълника три страни.

Формула обратна трансформация могат да бъдат получени поотделно или като последица от (1,17) и (1,18) чрез провеждане:

или чрез съпротивление:

Вследствие на това част от съпротивата на триъгълника е равна на сумата от съпротивленията на съседни точки на звездата, а произведенията им са разделени от съпротивата на третия лъч.