Урокът на алгебра в 8-ми клас на модула и квадратна функция
че "мнозина функции
Всеки може да се нарече ученик.
Но само няколко от днес
Решихме да ви кажа "
Проучването на квадратна функция модул ви позволява да задълбочи познанията на студентите в трансформацията на графики на квадратна функция. Учениците с голям интерес за извършване на даден модул задача. Посочените по-горе методи на диаграми функции са общи и се използват не само на площада, но и за други функции.
I. встъпителни думи на учителя
Функция - един от основните математически и научни понятия, които изразява връзката между променливите. Математика обмисля абстрактни променливи, изучава законите на връзката им, без ровене в същността на проблема. Например, в съотношение от Y = X 2 или математик инспектор виж зависимост от площта на квадрат от своя страна, и физика, самолет или корабостроител да видите връзка Y въздушно съпротивление сила или скоростта на водата от движение X.
Математически същите изследвания тази зависимост в абстрактна форма и го определя така, че увеличаване X 2 пъти Y ще се увеличи 4 пъти, и това заключение може да се прилага във всяка определена ситуация.
Модул и квадратна функция
Построяване функции:- Y = AX + BX 2 + C,
- Y = AX + BX 2 + C,
- Y = Ах 2 + Вх + C
II. орална работа
1) Определяне на броя на X модул
2) Определяне на квадратна функция, кажи всичко, което се знае за тази функция (структура свойства).
3) Намери фигура графиката на Y = Х + 4Х с 2 - 3.
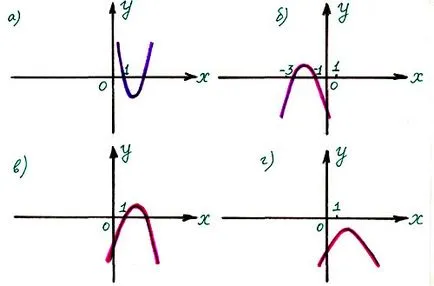
4) При това, което е показано на графиката на Y = - (X + 1) (2 - х)?
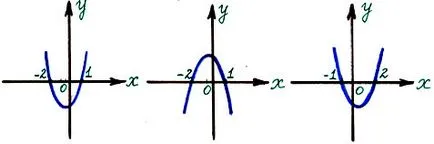
5) запомни как да се изгради графиката на Y = X
Чрез модул дефиниция
Графиката на Y = X е симетрична около оста Y.
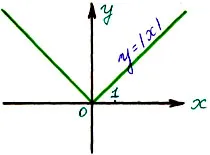
III. Построяване функции:
Работа, извършвана в групи, защото графики в K-1) и K-3) са едни и същи, те трябва да се сравняват и се направи заключение (на 3 групи). Всяка група е издадена карта в нея 3 работни места. Учениците трябва да конструират графики на квадратна функция, съдържащи модула, като се използва определението на модула и да се заключи, как да се конструира крива на функцията, използвайки графиката на квадратна функция и симетрия по отношение на координатните оси.
Задача. изграждане на графика на функция чрез използване на:
а) определяне на модула;
б) Графиката на функцията Y = Ах 2 + Вх + С;
в) по отношение на осите на симетрия.
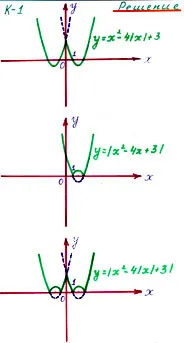
а) Y = X 2 - X 4 + 3
б) Y = X 2 - X 4 + 3
а) Y = X 2 - X 4 + 3
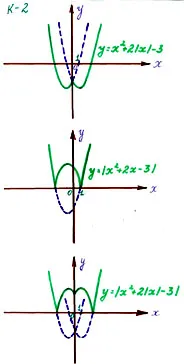
а) Y = X 2 + X с 2 - 3
б) Y = X 2 + X с 2 - 3
а) Y = X 2 + X с 2 - 3
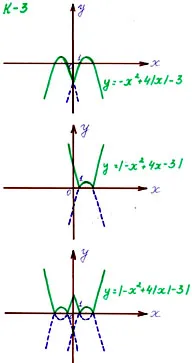
а) Y = Х + 2 X 4-3
б) Y = Х + 2 X 4-3
а) Y = Х + 2 X 4-3
IV. Учениците сключват аранжимент графики на тези функции
Въпрос: а) Как да се изгради графика на функция Y = F (X)?
(Метод 1. Парцел функцията Y = F (X), ако X 0 и Y = F (-x) когато X <0.
2 метод. Начертава се функция Y = F (X) и страничната дисплея полето генерирани симетрично около ос Y).
б) Как да се изгради графика на функция Y = F (X)?
(Построява функцията Y = F (X) и точката отрицателни координира дисплей симетрично около оста X).
в) Как да се изгради графика на функция Y = F (X)?
(Построява функцията Y = F (X), когато X е 0, и тази част на дисплея на графика симетрично спрямо оста Y, и след това отрицателно точка координира дисплея на симетрично спрямо оста X.)
г) Защо функциите на графични Y = -x 2 + 4Х - 3 и Y = X 2 - 4X + 3 са еднакви?
(Тъй като А = А -А = А)
Ние считаме, че функцията е независима променлива за маркировката за модул. А сега да разгледаме функцията, където има някаква самата функция или функция, и независимата променлива в даден момент, т.е. знак модул в зависимост от вида
Y = AX + BX 2 + С и Y = AX + BX 2 + C
Дайте конкретни примери.
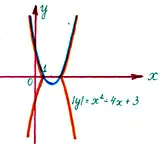
Построява се Y = F (X) функция и като тази част, която се намира над X оста като X 2 - 4X + 3 0 и към тях се прибавят относително симетрично картографиране ос X.
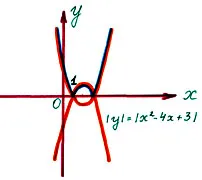
Първо, изграждане на графиката на Y = X 2 - 4X + 3. последвано от множеството от точки, чиито координати отговаря на условието за Y = X 2 - 4X + 3. т.е. графиката на Y = X 2 - 4X + 3 показва относителната ос X.
VI. творческа дейност
Предвид функция е Y = X 2 + 3 2X-
Изпълнете всички възможни трансформации на квадратна функция с модула.