свързан метод Gomory

Начало | За нас | обратна връзка

Проблемите с число за програмиране, за разлика от линейното програмиране проблеми, въведени допълнително ограничение на променливите: те могат да вземат само цели числа.

В някои приложения, като например тип превозно средство, това условие е изпълнено автоматично, ако изходните данни (брой на изпратени и получени стоки) се изразява чрез числа. Но в общия проблем за линейни техники за програмиране традиционните решения не гарантират число независимо от това дали интегралните или частични референтни стойности.

В математически нотация общия проблем за програмиране число е както следва:

Икономически линеен проблем програмиране често изисква решение число. Това се отнася до проблемите, в които променливи показват броя на неделими единици на продукти, оборудване, служители (проблемът с най-доброто разпределение на производствените поръчки между предприятия, проблемът за оптимизиране на производствената програма на отделните предприятия, оптимално оборудване и други задачи.). Често тези задачи се изпълняват в обичайния метод за симплекс, следван от закръгляне получените стойности на променливите, които ще числа. Но в този случай е възможно да се получи само приближение до наистина оптимален план число.

В друга група от задачи на линейното програмиране са определяеми количества капацитет най-ефективно предоставяне на предварително определена изискване. Тъй като "носители" на производствения капацитет на отделните предприятия акт, неделима част от оборудването, и така нататък .. Тези проблеми също са намалени до целочислени задачи на линейното програмен.

Също така е цяло число, рационално рязане материал триизмерна проблем (проблем за минимизиране на отпадъците), тъй като те представляват променливи са склонни брой изходни заготовки, се реже или друг начин.

Във всички тези задачи разтвор може да се намери чрез конвенционални методи линейно програмиране, с последваща корекция и получаване план число, повече или по-малко близо до оптимално. Но има и предизвикателства, които не са число решение, което няма смисъл. Те включват проблема за избор, в който числовите стойности на променливите се използват само за определяне на алтернативата ( "или - или", "да - не").

За модел число избор включват някои задачи оперативно-график, например, проблемът на оптимална последователност началото на различни продукти (части) на продукция. Да приемем, необходимо за определяне на реда старт н части, всяка от които е последователно обработени на няколко машини. Hij променливи равни на единство, ако част J трябва да бъдат управлявани от парче аз. и нула - във всички останали случаи. За всеки фиксиран й. както и за всеки аз. само един от наш променливи може да бъде равно на една, така че броят на ограничения на проблема, са следните:

Това свежда до минимум общото време за обработка на всички части на машините в групата. Non-число решение на този проблем няма смисъл.

Има няколко начина за решаване на проблемите число програмиране. Най-известният метод на Gomory. основава на използването на симплекс метод.

Помислете за математическите понятия: съгласуваността на цели числа, на число и дробна част от номера. Брой на еднакви номера б единствено и само ако разликата а - б е цяло число. Съответствие означават три хоризонтални тирета (≡); По този начин, ≡ б. ако - б е цяло число.

Всички числа са еднакви един до друг и са еднакви до нула. Не-целочислени елементи могат да бъдат представени като сума на цяло число и фракционна част от номер = [а] + а>. Скоби означават цялата част, сключено през тях, къдрава - като се дробна част от номера.

Свойства на еднаквостта на номера:

В решаването на проблемите число програмиране от Gomori първия етап съвпада с обичайната изчисляването на алгоритъма на симплекс. Полученият разтвор обикновено отговаря на всички условия на проблема, в допълнение към изискванията на пълнотата (това е възможно, разбира се, за да се получи разтвор число на първия етап). Ако между стойностите на променливите в оптималния план (точка А на фигура 13) е фракционна, е допълнително ограничение, като "прекъсване" дробна част от разтвора (линия 1 на Фигура 13), но оставя на място всички ограничения на проблема, който трябва отговарят на оптималния план. Допълнително ограничение е приложен към първоначалните ограничения на проблема и разширена система отново се прилага симплекс процедура. Ако оптималното решение отново ще бъде не-неразделна (точка В на фигура 13), след това се добавя един допълнителен ограничение (линия 2 на фигура 13) и на процеса на изчисляване се повтаря. Алгоритъмът позволява определен брой стъпки, за да стигне до оптималното решение на число (ако съществува) (точка С от Фигура 13).

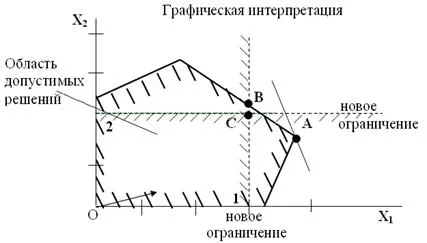
Фиг. 13. Метод съгласно съкращения Gomory

Пример за решаване число програмиране проблем. За да закупите оборудване за новия производствената площадка на 20 парични единици, разпределени Оборудването трябва да се приема на площ не повече от 38 m 2. Предприятието може да разпореди на оборудването на два вида: колкото по-мощна машина от тип А стойност 5 den.ed изискващи производство площ от 8 m 2 (обмислят пасове) и осигуряване на производителността 7 хиляди единици на смяна; по-малко мощни машини на стойност тип В 2 den.ed заема площ от 4 m 2 и 3, които дават промяна хиляди единици.

Необходимо е да се изчисли оптималния вариант на придобиване на оборудване, който предоставя данни при максимално ограничава цялостното изпълнение на обекта.

X1 е обозначен с броя на автомобилите, закупени чрез A и x2 - брой на придобитите машини B, ние получаваме математическите условията на проблема:

максимизира 7Н1 + 3x2 → макс

при условия: 5x1 + 2x2 ≤ 20

Използването на допълнително неравенството променлива x3 и x4 източник превръща в (предоставена на каноничната форма):

Ако основните променливи x1 и x2 - числа, уравнението следва директно като х3 променливи и х4 могат да вземат само цели числа.

Проблемът е решен първоначално без да се съобразява с изискванията на пълнотата.

Simplex маса е както следва:

оптимален план X1 В = 1, Х2 = 7,5; максимума на целевата функция е 29,5. Така, че е необходимо да купуват тип машина А и 7 машина тип В (8 машини нямат достатъчно пари или място), след изходния обем ще бъде F (х) = 7 х 1 + 3 х 7 = 28000. Единици ,

Намерете решение число от Gomory. Променлива X2. получи не-цяло число от гледна точка, е следното уравнение, което следва директно от горе симплекс таблица:

Това уравнение очевидно трябва да е вярно за валидно решение число.

Тъй Х2 - цяло число, тогава цялото е експресията на дясната страна на уравнение; Следователно, величината на дясната страна на това уравнение е лежи на нула:

Като се има предвид свойствата на горе еднаквостта и факта, че X3 и X4 - числа, експресията могат да бъдат превърнати до следното:

Тъй Х4 - неотрицателно цяло число, имаме:

0,25X4 = 0,5 или 1,5 или 2,5. ;

Това неравенство се трансформира в уравнението и се добавя към първоначалните ограничения система, която сега съдържа следните три формули:

Повтаряне на процеса на решаване на метода симплекс прилага на удължен ограничения система, ние получаваме нова оптимално план, в която стойностите на променливите, включени в основата са: Х1 = 2; Х2 = 5; Х4 = 2 (останалото свободно пространство).

По този начин, получени оптимално число решаването на проблема: ограничения на данни максималната производителност на (. 29 хиляди единици) при условие, 2 покупка тип А и тип Б машина 5 автомобила

Клон и пътуващ

Този метод може да се приложи за решаване на двете напълно и частично целочислени проблеми на дискретни програмиране.

Да приемем, че за всяко цяло число променлива, можете да зададете горна и долна граница, в която, разбира се, тя съдържа оптималните стойности

Обикновено Hj = 0, но това не е задължително. Проблемът се решава чрез метод симплекс. Ако Xk поема частични стойности, се смята, че оптималното решение на проблема, ще задоволи линейни ограничения Xk ≤ DK. или линейна ограничение Xk ≤ Dk + 1. където Dk = [Xk] - най-близкото цяло число по-малка част от XK стойност; Dk + 1 - най-близкото цяло число в голям начин от Хк. Така Hj ≤ Dk ≤ Vj - 1. След това е необходимо за решаване на няколко линейни програмни проблеми чрез симплекс метода:

Получават итеративния процес, представен като дърво, чиито връх съответства на разтвор на оригиналния проблема, и два клона, свързани с тях са разтвори на чифт линейно програмиране задачи А и Б. Полученият стойност на обективни функции в същото време може да бъде по-малка или равна на стойността на обективната функция на първоначалния проблем F ( X) А ≤ е (X) -0; F (X) B ≤ е (X) -0. Всяка една от двете нови клонове получи връх може да има по-нататъшното му разклонения.

1) итеративен процес продължава докато клон докато получи между планове се получава число разтвор, стойността на обективната функция трябва да бъде по-голям от или равен на стойностите на други функции целите разредителни възли.

2) Ако в следващия етап итерация двете имат не-число решения на проблема, избран връх съответстващ задача с по-висока стойност на обективната функция за допълнително разклоняване. За една от променливите, които са получили дробни стойности, събрани новите ограничения за следните линейни програмни проблеми.

3) Ако в следващия етап повторение, една от задачите има разтвор число и между стойностите на променливите в Вторият проблем, има фракционна, са избрани от задачата като най-високата стойност на обективната функция. Ако задача е получил разтвор число, процесът завърши, и ако задачата с частични стойности на променливите, процесът на допълнително разклоняване се извършва за нея.

4) Ако не сте в следващата стъпка итерация, една от целите на решението, а вторият проблем между променливите в получения разтвор е с частична стойност. След това, за първи процес разклонения задача се прекратява, и за по-нататъшно превръщане на втората задача е избрано едно от променливи не-число, за които са направени допълнителни ограничения за нов чифт линейни проблеми програмиране.

5) Ако в следващия етап повторение един от проблемите не е решение, както и за други полученият разтвор число, а има и други варианти с по-голямо число стойност на обективната функция, за които е възможно да се продължи разклоняване, процесът завършва и разтворът бе открита е оптимално число разтвор на оригинала задача.

Ако избраната задача води до счупване (задънена улица) или стойността на функцията по-малка от тази в проблем V.1f (X) A.4