Решаването на задачи на линейното програмиране графично

Определение. Всяко решение на системата от ограничения се нарича осъществимо решение ZLP.
Определение. Валидна разтвор, в който целевата функция достига максимална или минимална стойност се нарича оптимално решение.

От тези определения LP проблем може да бъде формулиран, както следва: за всички точки на изпъкналата региона, който е разтвор система ограничения за избор на тези координати, които минимизират (максимално) на линейна функция F = + s1x s2y.
Имайте предвид, че променливата х. Y в ZLP вземат обикновено не-отрицателни стойности (х ≥ 0, у ≥ 0), така региона се намира в квартал I координатна равнина.

Да разгледаме линейна функция F = + s1x s2y и да определи част от своята стойност Е. Да предположим, например, F = 0, т.е. s1x ​​s2y + = 0. графиката на това уравнение е линията, минаваща през произход (0, 0) (фиг.).
снимка
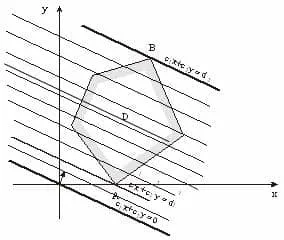
Промяната на тази фиксирана стойност F = г. направо s1x s2y + = г ще се измества паралелно и "zachertit" цялата равнина. Нека D - полигон - област решения ограничение на системата. При смяна на г линия s1x s2y + = г. за някои стойност на г = d1 Г. достигне тази точка се нарича "входна точка" на полигон А, и след това, преминавайки многоъгълник, по някаква стойност D = d2 ще имат с него последната обща точка се нарича V. В "изходна точка".
Очевидно е, че неговите най-малките и най-големите стойности на обективната функция F = + s1x s2y достигнат точки "вход" А и "изход" В.
Като се има предвид, че оптималната стойност на снимачната площадка на постижима решения функция може да отнеме във върховете на Г. може да предложи следното решение план ZLP:

1. изгради ограничения площ на разтворите;
2. изграждане на линия, съответстваща на целевата функция и успоредна превод на тази линия да се намери точка на "влизане" или "изход" (в зависимост от изискванията за свеждане до минимум или максимизиране на обективната функция);
3. определяне на координатите на тази точка, те се изчисли стойността на целевата функция.

Имайте предвид, че вектор (С1. C2), перпендикулярна на правата линия показва посоката на растеж на обективната функция.

В Графично решение ZLP два възможни случаи, които изискват специално внимание.

при 1

Фигура 6
При движение направо s1x s2y + = г «вход" или "изход" (както е показано) се появява на страната на многоъгълника. Това ще се случи, ако многоъгълника е страни, успоредни на линията + s1h s2u = г.
В този случай, точките "изход" ( "вход") безброй - а именно всяка точка на сегмента AB. Това означава, че целевата функция поема максимум (минимум) стойност не в една точка и всички точки, лежащи на съответната страна на многоъгълника D.

при 2
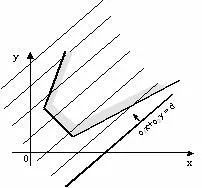
Да разгледаме случая, когато границите на допустимите стойности е неограничен.
В случай на неограничен област на обективната функция може да бъде определена така, че "изход" (или "запис"), съответстващ на това няма пряко точка. Тогава максималната стойност на (минимум) не се постига никога - да кажем, че функцията не е ограничен.

снимка
Необходимо е да се намери максималната стойност на обективната функция F = 4х + 6Y → макс. когато системата от ограничения
Ние изгради възможно регион, т.е. графично решаване на система от неравенства. За това ние изгради всяка линия и определят половината равнината, определена от неравенството.
х + у = 18

Построява линия, съответстваща F функция стойност = 0. 4x + 6Y = 0. ще се премести на линията по паралелен начин. От всички родове линии 4x + 6Y = конст последния връх, през които преминават директно на изхода на границата на многоъгълник ще бъде в горната част на С (12, 6). Той е тук, че F = 4x + 6у достигне максималната си стойност.
Следователно, когато х = 12, у = 6, функцията F достигне максималната си стойност F = 4 # 8729; 12 + 6 # 8729; 6 = 84, равно на 84. точка с координатите (12; 6) отговаря на всички системи неравенства ограничения, и в това стойността на обективната функция оптимално F * = 84 (оптималната стойност ще бъде означен с "*").
Проблемът е решен. Така че, е необходимо да се освободи 12 продукта тип I и 6 продукти от тип II, с печалба от 84 хиляди души. Разтрийте.

Графичният метод се използва за решаване на проблемите, които са имали само две променливи в система от ограничения. Този метод може да се прилага за системи за неравенството, с три променливи. Геометрично, ситуацията ще бъде различна, ролята ще се играе от пряк самолет в триизмерното пространство, както и решаването на неравенството на трите променливи ще бъде половин пространство, разположена от едната страна на самолета. Ролята на регионите ще играе полихедронов е пресечната точка на половин пространства.

влизане Правила данни

Задайте своите въпроси или да направите предложения или коментари могат да бъдат долната част на страницата в раздела Disqus.
Можете също така да изпратите заявка за помощ при справянето с изследвания на наши доверени партньори (тук или тук).