Приложение 2 пороен хиперболоидна на въртене - божествена пространство

платнища хиперболоидна

Ако линията за генериране на движение се върти около фиксирана права линия (ос), след това образува в този случай повърхността е споменатата повърхност на въртене. образуваща линия може да бъде плоска или пространствена крива и права линия.

Всяка точка на линия образуваща по време на въртенето около оста описва окръжност, която лежи в равнина, перпендикулярна на оста на въртене. Тези кръгове са наречени паралели. Следователно, равнина, перпендикулярна на оста на въртене се пресичат в повърхността на паралели. Линията на пресичане ротационна повърхност от равнина, минаваща през оста се нарича меридиан. Всички меридиани са еднакви на повърхността на въртене.

Множество от паралелно или меридиани е непрекъсната повърхност на въртене конструкция. Чрез всяка точка от повърхността минава един паралел и един меридиан. Предвижданията са разположени в съответните точки на паралелни издатини или меридиан. Посочете точка на повърхността или изграждане на втора проекция на точката, ако някой е настроен, можете да използвате паралел или меридиан, които преминават през този етап. Геометрична детерминанта част на ротационна повърхност на елемент на оста на въртене и образуваща линия.

Повърхностите образувани чрез завъртане на права линия:

1. - цилиндър въртене, образувана от въртящи се по права линия, паралелна на оста;

2. - конус на въртене, образувана от въртящи се по права линия пресича оста;

3. - листов хиперболоидна на въртене, образувана чрез завъртане на линия пресича с оста;

Успоредно на повърхността са кръгове.

Меридиана на повърхността е хипербола.

Всички управлявали повърхности е ротационна повърхност на втория ред.

Повърхностите образувани чрез завъртане кривите на втори ред около техните оси

1. Област на въртене е оформена по окръжност около нейния диаметър.

2. въртене елипсоид образувана от въртящи елипса около големи или малки ос.

3. въртене параболоид, генериран от въртене на парабола около оста си.

4. въртене хиперболоидна на един лист е оформена чрез завъртане на хипербола около своята въображаема ос (тази повърхност също е образувана от въртящи се по права линия: и п-1.).

Хиперболоидна на един лист е повърхност, каноничната уравнение има формата:

където, B, C - положителни числа.

Той има три равнини на симетрия, трите оси на симетрия и центъра на симетрия. Те са съответно на координатната равнина координатната ос и произхода. За да се построи хиперболоидна намерите раздел си в различни равнини. Ние намираме линията на пресичане с равнина XOY на. На тази равнина Z = 0, така че

Това уравнение определя равнина XOY на елипса с полу-оси А и В (фиг. 1). Ние намираме линията на пресичане на равнината yOz. На тази равнина х = 0, така че

Това уравнение за хипербола yOz равнина, където реално ос е равна на б, и въображаемата ос е равна на с. Ние изграждаме тази хипербола.

Напречно сечение самолет xOz като хипербола с уравнението

Draw и хипербола, но да не се претоварвайте рисуване допълнителни линии няма да изобразя нейния асимптота и премахване на асимптота сечение самолет yOz.

Намираме линията на пресичане на повърхността с равнините Z = ± з, з> 0.

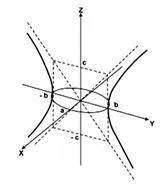
Фиг. 1. Напречно сечение на хиперболоидна на един лист

Уравненията на тези редове:

Първият уравнението във формата

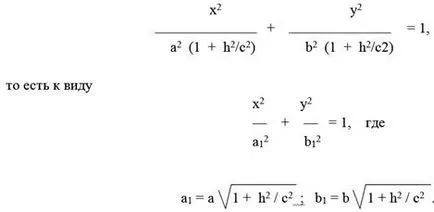
Това уравнение е елипса, подобен на елипсата в равнината XOY, с коефициент на сходство и semiaxes А1 и В1. Направи напречно сечение получава (фиг. 2).

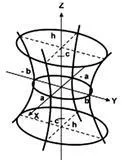
Фиг. 2. Изображение хиперболоидна за използване сечения

Листови хиперболоидна на въртене може да бъде получена чрез завъртане на права линия пресича с въображаемата ос, около която се върти тази линия. В този случай, пространствен образ (фиг. 3), на повърхността на който се състои от последователни позиции на линията на завъртане.

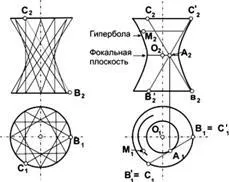
Фиг. 3. листов хиперболоидна на въртене, получена чрез завъртане по права линия се кръстосва с оста на въртене

Меридиана на такава повърхност е хипербола. Пространството вътре фигурата на въртене ще бъде валиден, а отвън - въображаем. Равнина, перпендикулярна на въображаемата ос и пресича хиперболоидна на един лист в нейната минимална раздел, наречен фокусната равнина.

Обичайно изображение око хиперболоидна на един лист е показано на фиг. 6.4.

Ако в уравнение А = В, след това хиперболоидна секционни равнини, успоредни на равнината XOY са кръгове. В този случай повърхността се нарича един листов въртящ хиперболоидна и може да бъде получена чрез завъртане на хипербола лежи в равнината yOz, около оста Оз (фиг. 4).

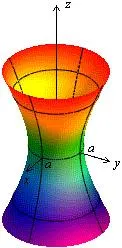
Фиг. 4. слоести hyperboloids на въртене,