Методи за превръщане метод чертеж за подмяна на прожекционни равнини на методи въртене методични

Често за шофиране прав, плоски форми или пространствена форма, в декларацията за поверителност, което е необходимо за решаване на проблема, е необходимо да се замени двете равнини на проекция. Преходът от V / H равнини на дадена система за новия V1 / H1 могат да се извършват по една от схемите, показани по-долу:

Фигура 12 е дадена точка А в системата на V / Н. След това, на прехода от система V / ч до V1 / H1 система. провежда ново ос на проекция X1, намерено нова проекция а1 точка А. Освен V1 / H система се заменя от нова система на прожекционни равнини V1 / H1 - вместо хоризонталната равнина на проекция въведе нов самолет H1.

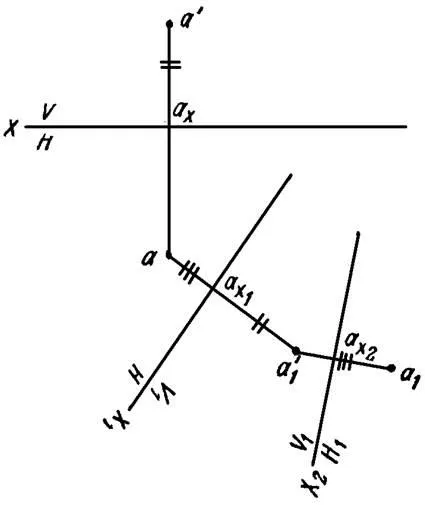
Позицията на нови оси на издатъците е избран в съответствие с конкретните условия на проблема.

Пример 6 За да се определи истинската формата на триъгълник ABC (Фигура 13).

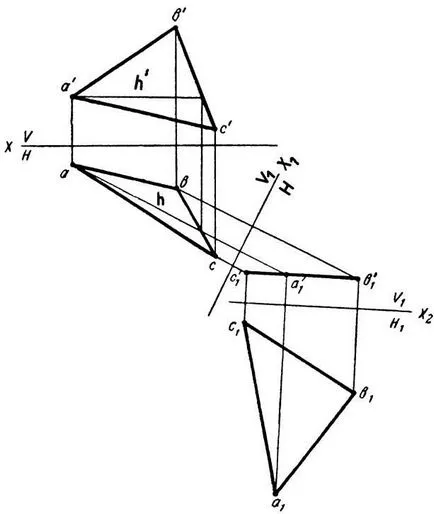
Триъгълник се проектира в пълен размер за всеки самолет на проекция, ако той е успоредно на тази плоскост. За триъгълника ABC се обърна успоредни една на прожекционни самолети, трябва да извършите двойно самолети заместване.

Моля замени V равнина на равнината V1. V1, перпендикулярна на равнината на триъгълника ABC избере равнина - нова проекция ос x1 трябва да е перпендикулярна на хоризонталната проекция на хоризонтална часа. Нов прогнози челен самолет триъгълник cproektiruetcya в права линия c'1 a'1 b'1. След това ще се въведе нов H1 проекция равнина, успоредна на равнината на триъгълника.

Приземен план a1 b1 c1 ABC триъгълник в новата система - истинската стойност на това.

Primer7. SAVS даден пирамида (Фигура 14). Определя се стойността на двустенен ъгъл на ръба AB.

Проблемът намалява с изграждането на ъгъла на прожектиране на равнината на проекция перпендикулярна на ръба.

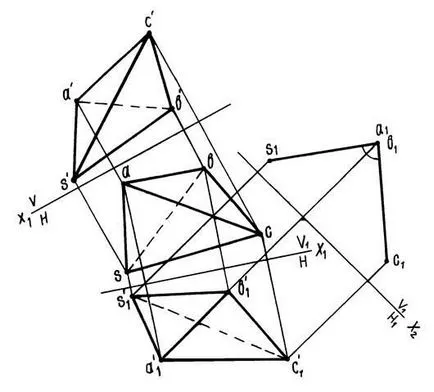
От ръба AB - права цялостното състояние, е необходимо да се направят две последователно заместване на проекционната равнина. равнина V се заменя равнина V1. успоредна на сегмента AB.

Ние считаме, нова предна проекция s'1 a'1 b'1 c'1 SAVS пирамида на нови прогнози за предна самолет. Тогава системата V1 / H да премине V1 / H1 система. Самолет H1 са разположени перпендикулярно на сегмента AB. На ръба на равнина H1 AB се проектира върху една точка, и лица и SAV SAV на - буквално. Ъгъл s1 a1 c1 се желае.

Primer8. SAVS даден пирамида (Фигура 15). Определете най-късото разстояние между ръбовете SA и пр.

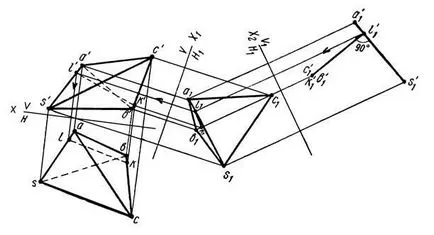
Direct SA и BC са кос. Следователно, проблемът се свежда до определяне на най-късото разстояние между две кос линии. За решаване на проблема е необходимо да се направи такава промяна в проекционната равнина, към новата система на една от линиите, като слънцето (Фигура 16), се оказа, перпендикулярна на равнината на проектиране. Замяна на равнината на проекция се извършва на V / H → V / H1 → V1 / H1.

Следователно, на методите за решаване на конверсия проблем е да се изпълняват четири основни стъпки:

1) директно преобразуване в директна родово ниво (за прави ъгли спрямо равнините на издатините и сегментите на първоначалния размер);

2. директно ниво на преобразуване в прожектираното линия (определяне на двустенен ъгъл, разстояние между редовете);

3. родово трансформация равнина в прожектираното равнина (равнина определяне ъгъл към равнината на проектиране, разстоянието от точката на равнината);

4. трансформира равнина на нивото на стърчащата равнина (равнината, определена от действителния размер).

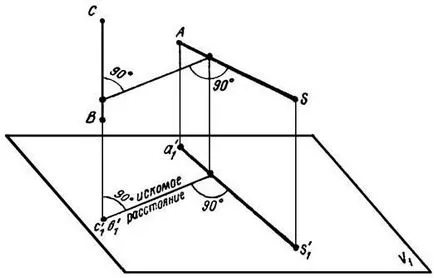
Системата V1 H1 пряка слънчева (вж. Фигура 15) се очаква да точка. Сегмент k'1 l'1 - най-късото разстояние между ръбовете на AS и пр. За да се конструира проекцията на късото разстояние в система V / H намери линия връзка точка L1 L1 К1 и изпълняват паралелно на оста Х2 на проекция, след което с помощта на комуникационни линии са основна проекция KL и k'l.

РЕЗЮМЕ методи въртене се състои в това, че предварително определена геометрична форма чрез завъртане на около ос се движи в пространството, доколкото той не взема определена позиция по отношение на непроменени равнини проекция на системата.

В зависимост от ротационната ос позиция по отношение на равнината на въртене на издатъците са следните методи:

а) се върти около ос, перпендикулярна на равнините на издатините;

б) същото без позицията на въртящи оси;

в) завъртане около хоризонталната или челната;

ж) въртящ се около една от релсите на равнина (подравняване).

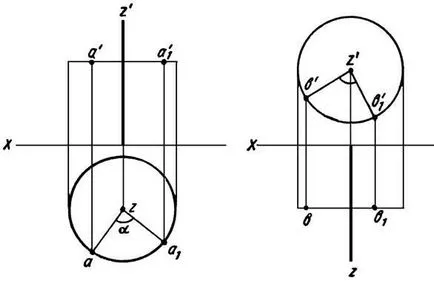
Фигура 17 Фигура 18

На диаграмата (Фигура 17) показва точка А и оста на въртене Z, перпендикулярна на равнината на проекция Н. По време на въртенето около оста Z. точка А ще се движи в кръг, разположена в равнина, перпендикулярна на оста на въртене (успоредна на равнината на проекция Н). Ако точка А се премества от положение А до позиция А1 г. Е. върти около ос Z, което при α ъгъл. след нейната хоризонтална проекция (а) да а1 позиция. описвайки дъга радиус ZA един (ZA - радиус на въртене) и изглед отпред (а) на мястото, ще се движи по права a'a'1. успоредно на оста X.

Ако оста на въртене Z (Фигура 18) е перпендикулярна проекция равнина V, след което точката се завърта около тази ос в предната проекция на траекторията ще се премести на обиколката и хоризонталата - линия, паралелна на оста X.

Пример 9. За да се комбинират точка А и равнината Р чрез въртящ се около ос Z предварително определено (Фигура 19).

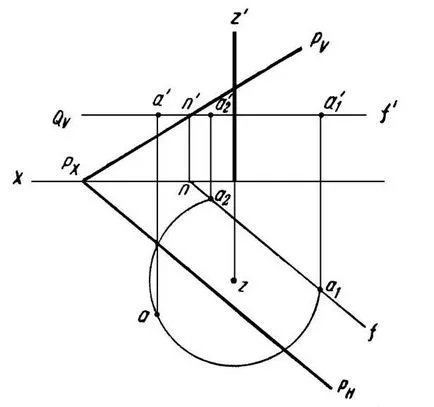
По време на въртенето около оста Z., точка А ще опишем кръг Р. равнина, перпендикулярна на тази ос. Равнината Q пресича равнината Р при предварително определено хоризонтално NF. Очевидно е, че точка А ще бъде в равнина Р, когато кръга, описан от точка А пресича хоризонтално NF. Задача, както е показано, има две решения.

За включване на линия AB (Фигура 20) в един ъгъл α, достатъчно, за да се превърне в предварително определен ъгъл, принадлежащи към две, то точка. От фигурата се вижда, че ABZ триъгълници и а1 b1 Z1 равни една на друга (от двете страни и на ъгъла между тях), но тъй като те са равни, следва, че AB = a1 b1, г. Е. Стойността на хоризонталната проекция на сегмент по време на неговото въртене около оста, перпендикулярна Н не се променя, само променя позицията си спрямо оста на координатната. Това обстоятелство дава възможност да се опрости конструкцията на пример в борбата с

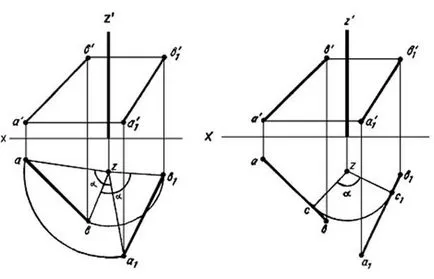
Фигура 20 Фигура 21

Фигура 21 да се върти около линия AB Z ос под ъгъл от α Z, пропуска перпендикулярна аб. След това, точката се върти с предварително определен ъгъл α, С1 точка чрез ред е съставен перпендикулярна на радиус С1 Z на, и забавени сегменти C1 а1 = ва и С1 b1 = CB.

Въртенето на равнината около ос, перпендикулярна на равнината на проектиране, се извършва чрез завъртане на същия ъгъл в същата посока точки и линии, където предварително определената равнина.

Фигура 22 равнина определена от триъгълника ABC се завърта около оста Z. позиция перпендикулярна предна равнина (хоризонтална проекция на хоризонтално положение A1 взети перпендикулярна на оста X).

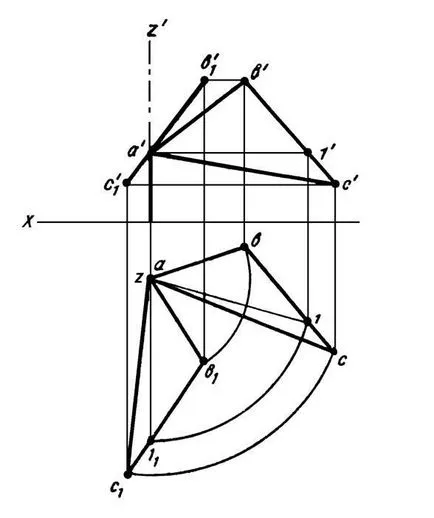
Ако равнината, определена парчета, след това за равнината на завъртане под ъгъл трябва да се върти с предварително определен ъгъл от един от нейната хоризонтална или следи и тази предна равнина (фигура 23).

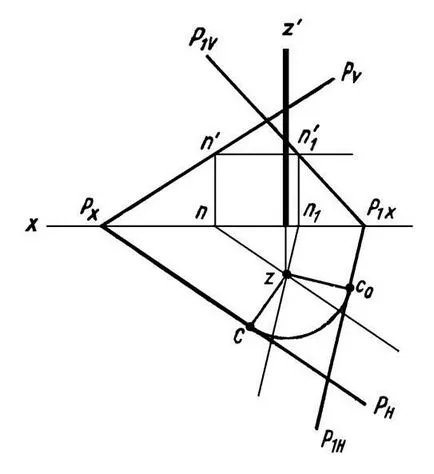
По този начин, по време на въртенето на всеки пространствен форма около ос, перпендикулярна проекция равнина, неговата проекция на равнината на неговата величина не се променя. Ще се промени само позицията на проекция спрямо оста на координатната. Възползвайки се от това, за решение на даден проблем можем да приложим метода на въртене, не е показано на чертежа, осите на въртене.