методи за оптимизация в голям размер на проблема
метод на разпадане на базата на агрегация в голям мащаб проблеми
въз основа на сумирането на метод разлагане в нелинейни проблеми за програмиране
системи за разлагане
Принципът разлагане (или както се нарича принцип децентрализация) е да разделя системата на подсистеми с желани свойства. Този метод се използва за обосновка йерархична изграждане на комплексни системи, по-специално за изследване на различни модели на взаимодействие между нивата между нивото на икономически системи за решаване на оперативни задачи за управление и планиране.
При прилагането на проблемите на разлагане на оптимизация е за разделяне на основната задача на подзадачи значително по-малък размер, което може да бъде решен чрез съществуващите средства.
Тези подзадачи образуват първата йерархична система ниво, създадена за изчислителни цели.
На първото ниво са решени подзадачи в произволни връзки. Определяне на тези отношения е задача на второто ниво.
Липса на централна контролен орган подробна информация за производствените възможности на отделните подсистеми налага йерархична структура, в която дружеството-майка, събира някои обобщена информация за подчинените му подсистеми и след това го освобождава в една или друга форма посочване на желаното или се очаква от дейността им. След като прочетете тези инструкции, подсистемата може да управлява най-добрите "насрещни планове", в която най-добрият начин те са взети предвид техните интереси.
Въз основа на тази информация, централното тяло се приспособява своите насоки, както и процесът се повтаря до окончателното споразумение.
Отличителна черта на много практически проблеми на научните изследвания е тяхната голяма измерение. По-специално, при решаване на проблемите на оптимално планиране за макро измерение ограничения матрица достигне 10 4 -10 5. В този размер класически математически методи за програмиране (линейни, нелинейни, дискретно) са неефективни. Т.е. ние се сблъскваме тук с феномена на "проклятие на размерност" разбиране R.Bellmana.
Това е наложило разработването на специални техники като точна и приблизителното предназначен за мащабни проблеми. Повечето от тези методи се основава на концепцията на разлагане, което е в разчленяването на първоначалния проблем на едрогабаритни, намирането на независими решения за всеки един от тях и след това да се свържат тези конкретни решения в общото решение на първоначалния проблем. Идеята на разлагане по отношение на проблема с LP е формулирана G.Dantsigom и Wolf, и по-късно е разработена в D.B.Yudina, B.G.Golshteyna [12] М. Mesarovich, L.Lesdona [31] V.Tsurkova [52], и други.
Методът на разлагане Dantzig-Wolfe
G. Данциг през 1960 г., и метод Wolfe разлагане разработени решения за високи размерите проблеми със специална структура на матрицата на ограничение [31].
Този метод е най-ефективен за решаване на проблемите, ограничение матрица, която има блок диагонал форма с малък брой променливи. Въпреки това, както се вижда от по-нататъшни изследвания, методът е приложим за LP проблеми с общата форма на матрица също. Методът съответстващ е предвидено D.B.Yudinym и E.G.Golshteynom нарича "програмен блок" [12].
Отличителна черта на метода на разлагане е използването на дадена задача координираща институция. който има, в сравнение с оригинала, малък брой редове и голям брой колони.
От съществено значение е, че не е необходимо да се уточни всички колони изрично за справяне с проблема с координацията. Те се образуват в процеса на използване на метода на симплекс. Такъв подход се нарича метод колона поколение. Същността му е, както следва. Да бъде видове LP проблем:
Да приемем, че допустима известен основния разтвор (DBR) XB и съответната матрица на база vektorovA. Да приемем, също така, че XB е намерено от инверсната матрица. Тогава там е намерен в същото време и вектора на относителните оценки
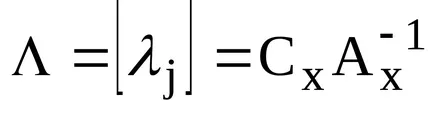
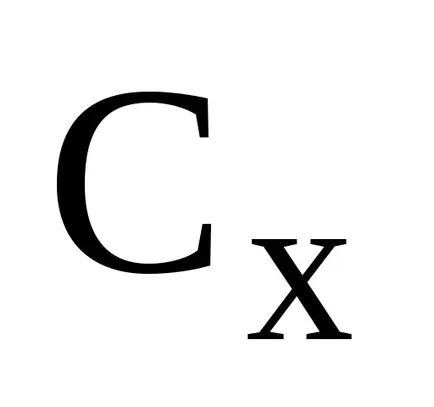
За определяне на възможностите за подобряване на XB DBD за всеки nonbasic vektoraAj изчислена стойност за оценка на:
Ако първоначалният разтвор може да се подобри чрез въвеждане на променлива основа XS. Въпреки това, ако има голям брой nonbasic колони (n10 3), от nahozhdenieS vychisleniyaj вектори за всички nonbasic
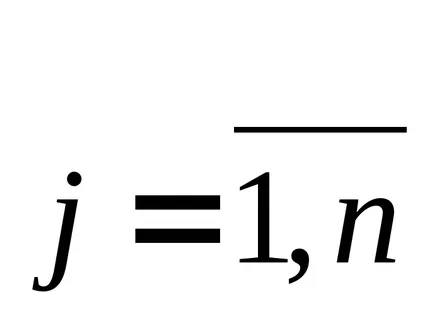
Ние приемаме, че всички колони AS избрани от изпъкнала mnozhestvaS. дефинирана система от уравнения и неравенства. Тогава векторът на колона, за да се вписват в основа, може да се определи чрез решаване спомагателен проблем на формата:
където
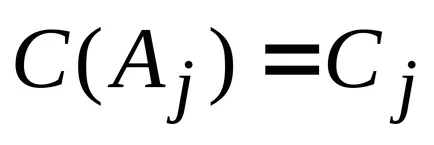
Този процес се нарича с генерирането на колоната. тъй като в разтвора на проблема (4) е всъщност използва само малък брой колони се генерира както е необходимо.
Това значително намалява необходимия капацитет памет за съхраняване на текущото ниво, което е значително предимство при решаване на големи проблеми.