Как да намерите областта на Пентагона

3 Процедура: площ OsnovyVychislenie петоъгълник: площ geometriyaVychislenie петоъгълник: формула

Част 1 от 3: Основи

1. 
   1 Редовна и неправилен петоъгълник. Редовен петоъгълник - петоъгълник, в който всички страни са равни; в противен случай Пентагона нарече погрешно.
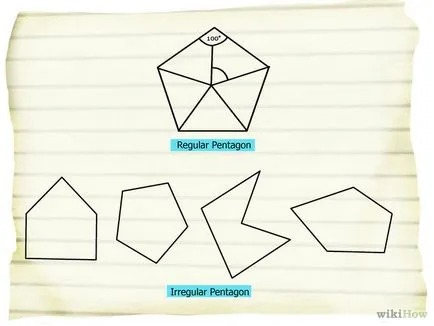
   • Редовен петоъгълник винаги ще изпъкнал (вж. По-долу). Грешен петоъгълник може да бъде изпъкнала и вдлъбната.
2. 
   2 изпъкнал и вдлъбнат петоъгълници. Изпъкнал петоъгълник все още няма върховете навътре насочени форма (с други думи, има без вътрешни ъгли по-голям от 180 градуса). Вдлъбнатата петоъгълник има връх насочен навътре фигура (с други думи, има вътрешен ъгъл по-голям от 180 градуса).
3. 
   3 периметъра на петоъгълник. Както и в случая на други геометрични фигури, за да се намери периметъра на Пентагона е лесно: просто добавете дължина на всички пет страни.
4. 
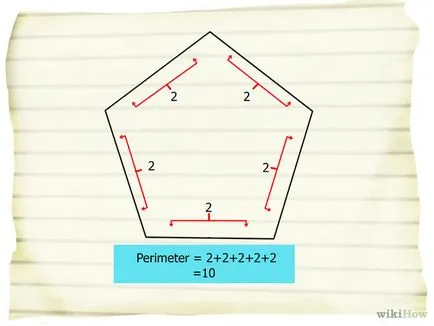
   4 Апотема равностранен петоъгълник. Апотема - сегмент, свързваща центъра на Пентагона и в средата на всяка от страните.
5. 
   5 Основни тригонометрични функции. Те трябва да знаят, като площта на Пентагона може да се намери чрез нейното разпадане на правоъгълни триъгълници. Има три основни тригонометрични функции: грях ъгъл = срещу крака / хипотенуза; = Защото ъгъл съседна страна / хипотенуза; TG = ъгъл срещулежащ катет / съседна страна.

Част 2 от 3: Изчисляване на областта на петоъгълник: геометрия

1. 
   1 Разделете петоъгълник в пет равнобедрен триъгълник. След това, във всеки триъгълник по-ниска височина (от центъра на Пентагона). Вие ще получите десет правоъгълен триъгълник. Не забравяйте, че всеки ъгъл на Пентагона е 108 °.
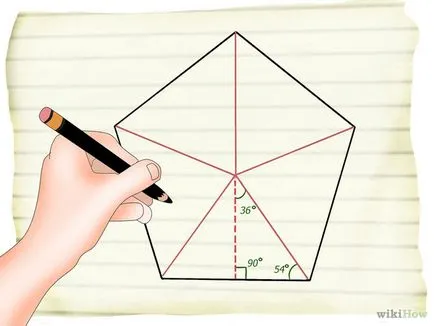
   • Например, да се намерят лицето на редовен петоъгълник със страна 6 см. За да започнете да го прекъсне, както е показано на фигурата.
2. 
   2 Откриване на страната на равнобедрен триъгълник. За да направите това, помислете за един от правоъгълни триъгълници.
   • В този пример страничен петоъгълник е 6 cm. Следователно, един крак на правоъгълен триъгълник е равна на 3 cm (като посоката на височина разделя наполовина на петоъгълник). Използването на тригонометрични функции може да се изчисли от другата страна. Изчисленията са показани на Фиг.
3. 
   3 Изчислете областта на правоъгълен триъгълник. Площта на правоъгълен триъгълник се изчислява по прост формула: А1 = AB / 2.
   • В горния пример, да бъде заменен, намерени в тази формула стойности. Изчисленията са показани на Фиг.
4. 
   4 Намерете областта на Пентагона. Припомнете си, че сте счупи петоъгълник десет правоъгълен триъгълник. Така, общата площ на петоъгълник е десет пъти по-голяма от площта на правоъгълен триъгълник: А = 10 * A1.
   • В горния пример зона петоъгълник се изчислява, както следва: А = А1 = 10 * 10 * 3,0321 = 30,3210.

Част 3 от 3: Изчисляване на областта на петоъгълник: формула

1. 
   1 Формулата за изчисляване на площта на правилен многоъгълник: А = PA / 2, където Р - периметъра на многоъгълника, и - Апотема многоъгълник.
   • Например, даден равностранен петоъгълник със страна 6 см. Намерете своя район.
2. 
   2 Намерете периметъра на петоъгълник. За да направите това, добавете дължините на всички свои страни.
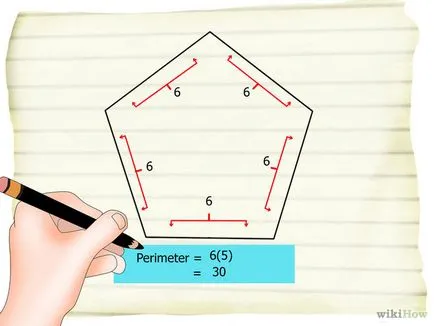
   • В горния пример: R = 6 + 6 + 6 + 6 + 6 = 30.
3. 
   3 Откриване apofemu петоъгълник. Ако знаете на страничен многоъгълник, тя Апотема изчислява по формулата: А = S / 2tan (180 / N), където S - страна на многоъгълника, п - брой страни на многоъгълника.
   • В примера по-горе изчисляване Апотема показано.
4. 
   4 изчисляват областта на петоъгълник. За това се използва основната формула за изчисляване на площта на петоъгълник.
   • В горния пример, А = (30 * 2,0214) / 2 = 30,3210.

• Ако е възможно, се изчислява площта на петоъгълник, като се използват и двете описания метод. След сравняване на резултатите, за да потвърдите правилния отговор.