изрази за преобразуване, съдържащи радикали

§ 42. Преобразуване на изрази, съдържащи радикали

В 7 и 8 клас сте завършили трансформацията на рационални изрази с помощта на правилата за работа на полиноми и дробни числа, формули за съкратено умножение и т.н. В 8-ми клас, научи нова операция - операция за извличане на корен квадратен от неотрицателно число и при използване на свойствата на корен квадратен, извършва конвертиране изрази, свързани с квадратни корени. В предходните раздели сме изпълнени с извличане корен операция на тото степента на реално число, изучава свойствата на тази операция, а именно (за не-отрицателни стойности на А и В):

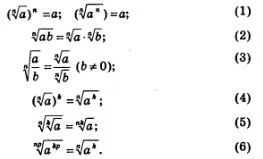
Използването на тези формули, е възможно да се изрази преобразуване съдържащи операция екстракция корен (изрази радикали), - изрази наречени ирационално. Помислете за няколко примера за ирационални изрази реализация.
Пример 1: Опростяване на израза:

Решение: а) представлява radicand 32а 5, когато 16 и 4 - 2а и използването на формула (2); получаваме:
Полученият израз се счита за по-лесно от снимачната площадка, защото по силата на радикала съдържа повече от един прост израз. Такава трансформация се нарича налагането на фактор в знак на радикала.
б) Използване на (4), получаваме:

Представлява radicand и 10 под формата на 9-а и използването на формула (2); получаваме:

Както можете да видите, и тук е в състояние да направи знака на множителя за радикала.

Не забравяйте, че формулата сте учили в хода на алгебра в 8-ми клас. Той се отнесе за всеки дори и индекса на корен
Тази формула трябва да се има предвид в случаите, когато не е сигурно, че променливите отнеме само не-отрицателни стойности. Например, въвеждане на фактор за знака на корена в експресията. трябва (ако знака на х не е известен), за да се твърди, както следва:

В допълнение към въвеждането на фактор като знак на радикала, когато е уместно, използване и преобразуване, така да се каже, на обратната посока: въвеждането на фактор под радикал знак. Тази трансформация, се използват следните два примера.
Пример 2. За сравнение на броя
Решение. В момента има:

ПРИМЕР 3 Опростена експресия
Решение. Първи фактор ще направи 1 х по степен на корен знак трета:

Сега даден израз може да се запише като:
Като се използва формулата (5), можем да запишем последния израз под формата

Пример 4. Извършете стъпки:

Решение: а) можете да приложите формулата за намаляване умножаване на "разликата от квадратите":

Използване на формула (6), за да разделят всеки от индексите на основните получени радикали и radicand е 2; Това значително ще опрости вписване:

б) Възможно е да се прилагат формулата на съкратена умножение "Разлика кубчета":

Пример 5. Извършете стъпки:

Решение: а) Тъй като можете да се размножават само корените на същата степен, ние започваме с параметрите на настройка в наличните радикали. За тази двойна употреба формула (6):

Сега ние използваме формула (2):

Остава да се направи знака на множителя за радикала:

б) Първият начин. Трансформирайте първия фактор на основата на 4-то степента:

Вторият метод. Ние работим първо с radicand във втория фактор. В момента има:

Разделяне на основата на изпълнение и радикал експресия с 2, ние получаваме: (формула (6), ние тук има право да използва, както радикал изразяване - положително число). Остава да се размножават квадратни корени:

Пример 6. фактор:

Решение. Предвид експресия може да бъде пренаписана, както следва:
Сега ние виждаме, че това е - точен квадрат, на площада на разликата между изразите
И накрая, ние се получи:

Пример 7 За да се намали фракция
Reshenie.Pervy метод. В знаменателя може да се трансформира, както следва:

Така че има причина да представят в числителя като "разлика от квадрати":

Вторият метод. Въвеждаме нови променливи:

Това ни даде промяната на променливите? Тя нека замени ирационален израз (с променливи х и у) е рационален израз (с променливи А и В). И работи с рационални изрази е много по-лесно, отколкото с ирационалното. В момента има:

AG Mordkovich Алгебра 10 клас

Ако имате корекции или предложения на този урок, моля свържете се с нас.

Ако искате да видите и другите корекции и предложения за уроци, погледнете тук - Образователен форум.