Изчисляване на линейна индуктивност и капацитет за единица дължина на предаването линия

Капацитет за единица дължина на предаването на лентата линия с изключение на случайни полета. Фиг. 3 показва предаване линия лента с диелектрик пълнене и разпределение и elektricheskogoE magnitnogoN полета в съответствие с изключение на случайни полета. Електрическото индуцирането между електродите на предаването линия се определя като

, gde- относителна диелектрична константа на материала запълване на пространството между електродите на предаване линия.

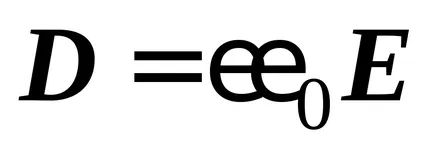
повърхностна плътност ZaryadaQpov на вътрешните повърхности на електродите е на електрическа индукция (формула (4)). Таксата се съхранява на вътрешните повърхности на електродите:

където т и л - съответно ширината и дължината на линия електрод предаване.

Потенциалният разликата между електродите

От уравнение (1) експресира капацитет на предаване линия:

След заместване с формули (13) и (14) с (4) в (15) намираме лентовата система на капацитета :.

Осъществяване на намаляването на Е. накрая получаване на:

. По този начин, ние имаме капацитета на сегмент dlinoyl преносна линия.

Капацитет на единица дължина - това е капацитета на дължината на преносната линия на устройството. Означаваме капацитет на единица дължина, направени от С1 = C / л. В съответствие с това определение, получаваме:

Отчитане на бездомни полета доведе до увеличаване на капацитет на единица дължина, тъй като предварително определена потенциалната разлика се дължи на случайни полета произвежда допълнително заплащане на страничните повърхности и външните повърхности на електродите. Получената формула (16) за капацитет на единица дължина с изключение на случайни полета дава стойността на капацитет на единица дължина, по-близо до действителната стойност, по-голяма съотношението тегло / г. Точна разтвор на линия капацитет на предаване лентовата на единица дължина се получава чрез преобразуване конформна.

Индуктивност предаване лентова система с изключение на бездомни полета. Да разгледаме една лентова електрод и на магнитното поле, създадено от тока, протичащ в електрода (фиг. 4).

Нека бездомно поле извън вътрешното пространство на предаването линия е нула, тогава изчисляването на интеграла трябва да се разглежда само в рамките на област линия. Поради това, в съответствие със закона на Ампер общия ток (

):.

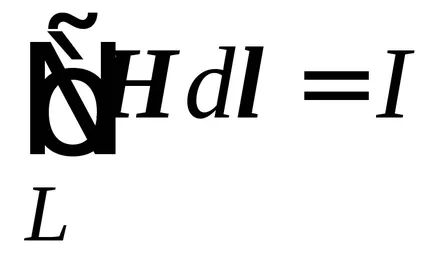
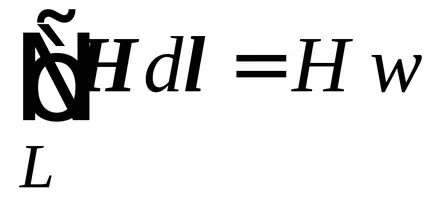
По този начин, в случай на пренебрегване на бездомни областта на общия ток трябва закон на Ампер

Потокът на магнитната индукция в пространството между електродите лентовата система

Във формула (18) S - площ на електрода.

Заместването в (18), изразът (17) и като се вземе предвид, че магнитната индукция между електродите

, получаваме

От (19) следва, че индуктивност на линия дължина сегмент л :.

Съответно, индуктивност на единица дължина на предаването линия с изключение на случайни полета.

Отчитане на бездомни полета доведе до намаляване на индуктивност на единица дължина, тъй като за даден ток поради бездомни областта на магнитен интензитет на поле попада между редовете и електродите съответно се намалява потока на магнитната индукция в пространството между електродите. Получената формула за индуктивност на единица дължина и изключват бездомни областта ще индуктивност стойност на единица дължина, по-близо до действителната стойност, по-голяма съотношението тегло / час.

Капацитет за единица дължина на коаксиален предаване линия. Фиг. 5 показва напречно сечение на коаксиален предаване линия dlinoyl на.

Най-

коаксиален далекопровод не бездомни полета. При изчисленията, ние приемаме, че електрическите и магнитните полета не проникват в проводник (електрод) материал. Това предположение е вярно, ако проводниците са изработени от материал с висока provodimistyu (мед, свръхпроводник-Vodnik) и заедно с това rassmarivayutsya поле различни по време на висока честота, която осигурява ниска дълбочина на проникване в материала проводници поле veniya.

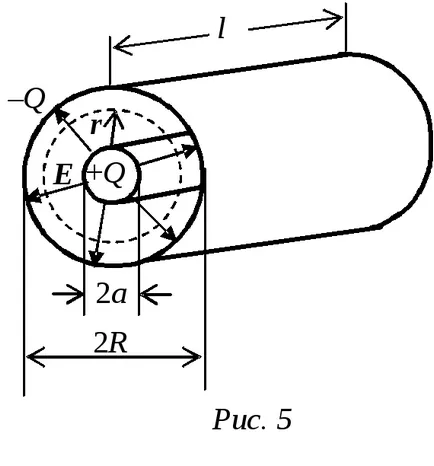
Нека между вътрешните и външните проводници действат U. разлика потенциали на електродите и натрупаната zaryadQ.

Помислете за вътрешния проводник. Ние обграждат своята цилиндрична повърхност с радиус R. като ploschadSts =

. Чрез този поток прониква повърхността на електрическа индукция е числено равно на заряд центриран вътрешна повърхност. Тогава според теоремата на Гаус ():

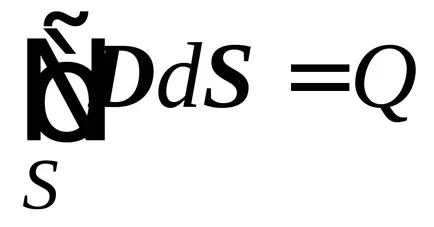
изрази (20) електрическа индукция

От израза (21), като се вземат предвид

намерите електрическото поле в качеството между електродите:

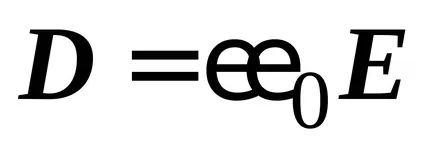
Ние считаме, потенциална разлика между електродите на коаксиален линия:

Замествайки в (23), изразът за напрегнатостта на полето (22) и се изчислява на интеграл:

.

Следователно ние получаваме на капацитета на коаксиален дължина линия L и, съответно, капацитет за единица дължина на коаксиален линия.

P

Fire индуктивност коаксиален предаване линия. Фиг. 6 показва магнитно поле разпределение в напречното сечение на коаксиален предаване линия. Използването на закона общият ток на Ампер, ние откриваме, че силата на магнитното поле между електродите на коаксиален линия. Както интеграция верига изберете радиус R кръг. чиято дължина е равна 2πr. като има предвид, магнитен интензитет на полето:

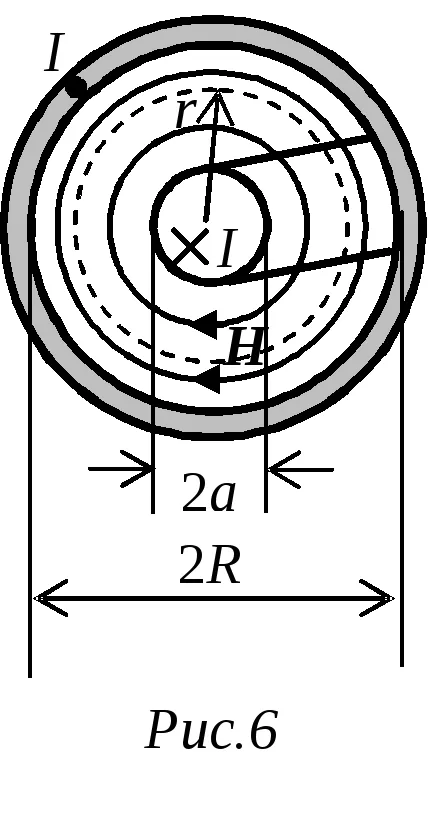
където I - ток в центъра диригент.

Магнитна индукция между електродите на коаксиалната линия с израза (24)

Вземете интеграл на вектора на магнитната индукция (25) по дължината на линията от 0 до л и радиално ОТА Дор. В резултат на интегрирането, ние получаваме общия поток на магнитната индукция:

От (26) се получава стойността на индуктивността на дължина линия L коаксиален като коефициент на пропорционалност между потока на вектора на магнитната индукция и широка ток:

Съответно, намаляване (27), за да л. Качваме се на индуктивност на единица дължина от един коаксиален кабел.

Относителната магнитната проницаемост на материала запълване на вътрешното пространство на предаването линия на микровълнови честоти почти винаги е равна на нула. Това твърдение не се отнася за случая на магнетизираната феритни - материал, който има широко приложение в микровълнова технология. Магнитна проницаемост ферит анизотропна, т. Е. Това зависи от посоката, в която са разположени векторите Н и B. Преди получен формула за случая на преносни линии, пълни с магнитни ферити, не са приложими.