Глава 1 в електростатично поле вакуум
1 Електрически заряд. закона на Кулон
Вече е известно, че в основата на всички природни явления от многообразието на базата на четирите фундаментални взаимодействия между елементарните частици - голямата ядрена, слаба ядрена, електромагнитното и гравитационното. Всеки тип на взаимодействие, свързано с определени характеристики на частиците. Например, гравитационното взаимодействието зависи от масите на частиците на електромагнитни електрически заряди.
Свойства на електрически заряд:
1. електрически заряд съществува в две форми: като положителна

2. Във всеки електрическа система изолиран алгебричната сума от такси не се променя - това твърдение vyrazhaetzakon опазване на електрически заряд.
3. Всички такси

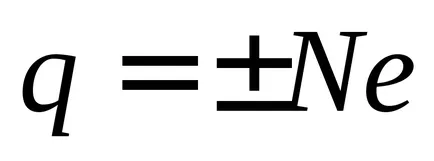
4. електрическия заряд е релативистично инвариант. стойността му не зависи от скоростта, с която тя се движи. Това означава, че размерът на такса измерва в различни инерционни еталонни системи е един и същ.
закона на Кулон
Ако начислява размера на тялото е нищожен в сравнение с разстоянието до други органи, такъв орган се нарича такса точка. Законът на взаимодействие на точкови заряди Експериментално е установено от френския физик Шарл Кулон през 1785.
закон гласи, Кулон. че силата на взаимодействието на две стационарни такси точка във вакуум е пропорционално на количеството на заряд
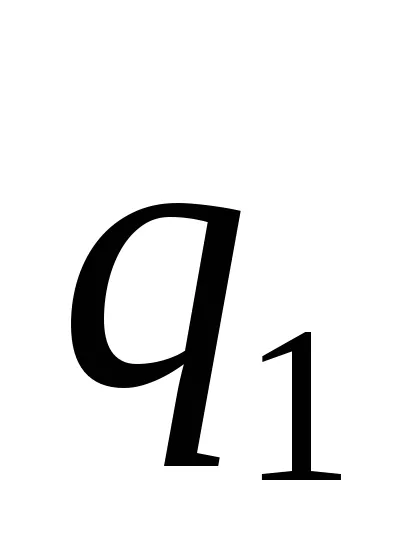
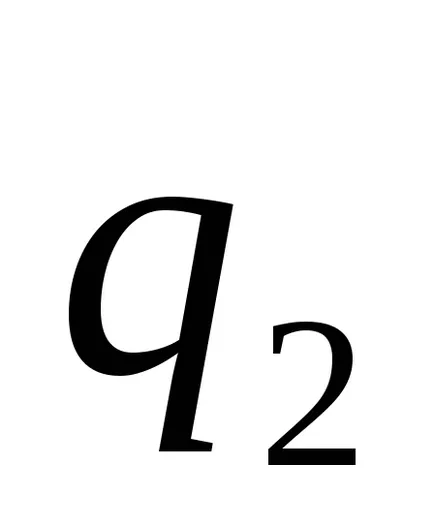
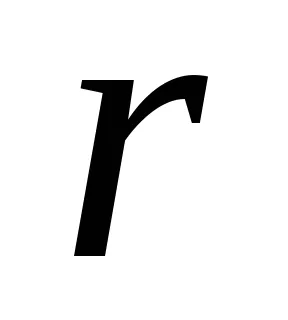
където
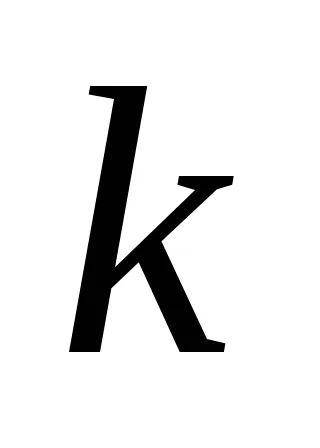
Силата е насочена по линията, съединяваща тези такси, и като такси отблъсне и за разлика от привличане.
закона на Кулон може да се изрази във векторен вид:
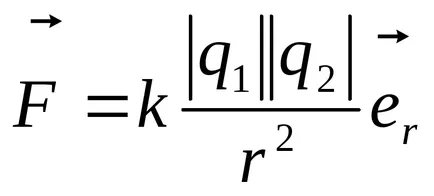
където
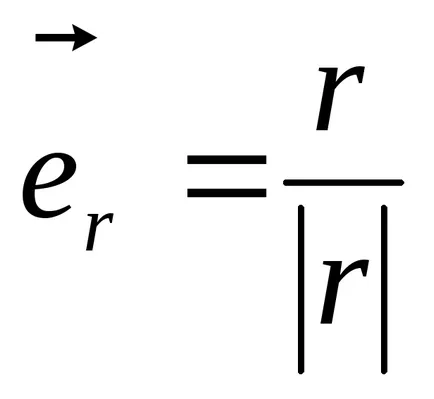
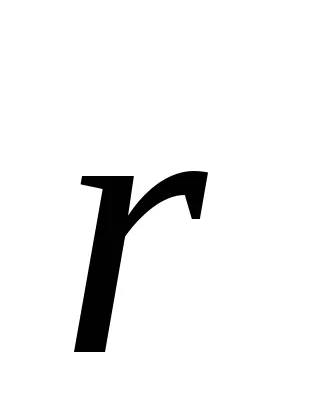
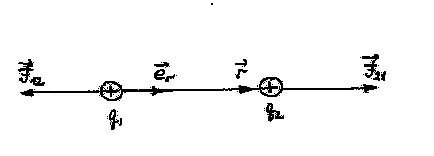
Фиг. 1 показва силата на отблъскване на двете положителни заряди.
В системата на CGS
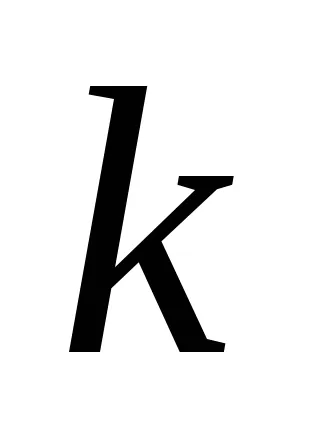
Международната система единици (SI) единица заряд - Медальон коефициента
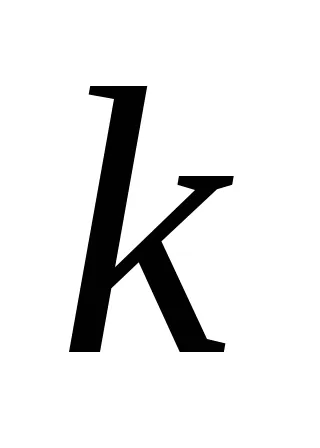
Той е представен като:
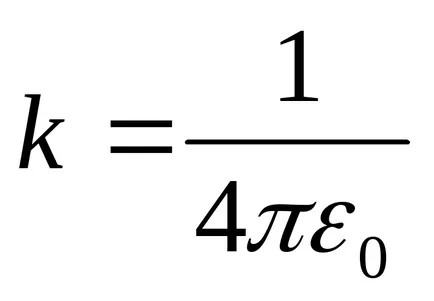
След това, с формула изразяване на закона е, както следва:
стойност
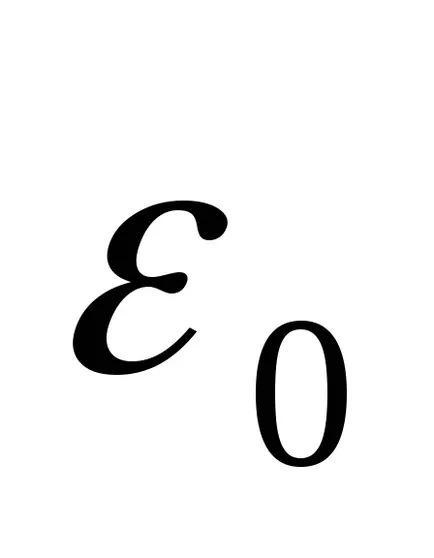
Когато F (фарад) - единица капацитет
(1.1), (1.2) и (1.3) изрази закон на Кулон във вакуум. Въпреки това, ако електрически заряди са в среда, която се характеризира с относителна диелектрична


принуди принципа на суперпозиция
Да предположим, че в допълнение към таксата

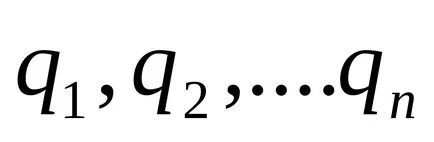
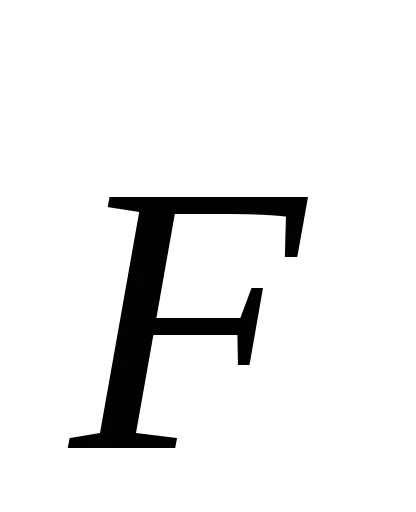

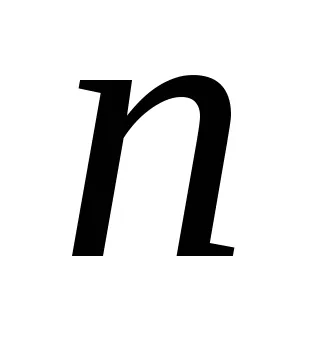
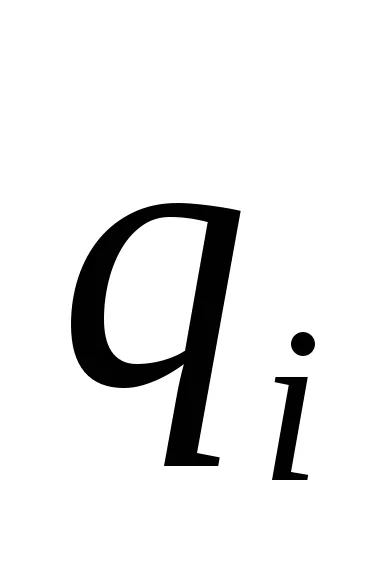
където
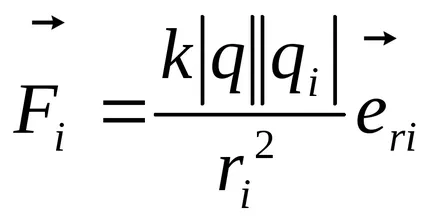

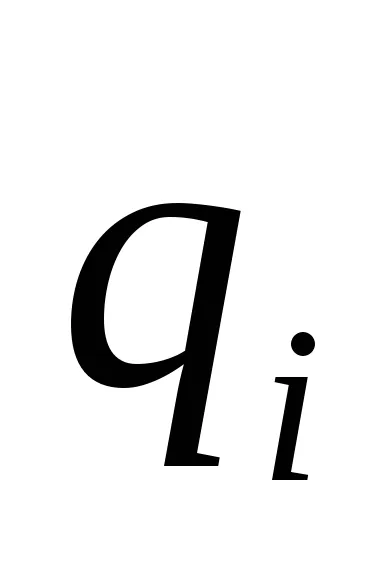
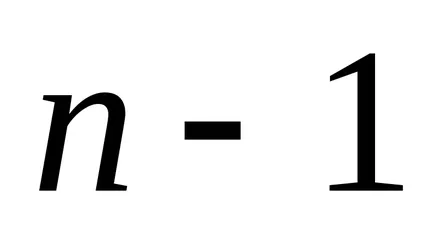
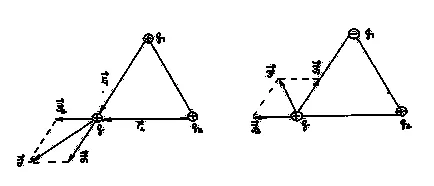
Примери за намиране на резултантната сила