Формула ускорение по физика
Ускорение (моментално ускорение) е векторът, който определя скоростта, с която се променя движи скорост на материал точка.
Обикновено означават ускорение. В теоретична механика отговаря определянето на ускорение :. Математическият определението на моментната ускорение е израз:
където - скоростта на движение на материална точка
при което - радиусът - вектор, който определя позицията на материална точка в пространството.
Ускорение вектор се намира в равнината на контакт, при което основните е нормално и допирателна към траекторията, по този начин има посока към вдлъбната крива.
Единици за измерване на ускорението
Основните звена на ускорение в SI единици е: [а] = м / 2
видове ускорение
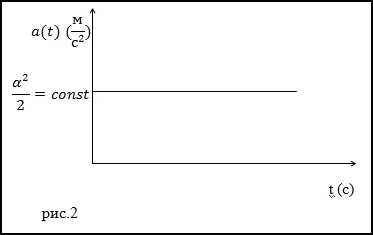
Ако изгради допирателна равнина във всяка точка на траекторията, векторът се разлага в две перпендикулярни компоненти:
където - вектор, насочена по нормалата към основен център на кривината на траекторията на материал точка - това е нормално ускорение; - вектор насочени по допирателна към пътя - е тангенциално ускорение. В този случай, следните уравнения притежават:
при което - величината на скоростта, R - радиусът на кривината на траекторията, по - проекция вектор върху единичен вектор основната нормална AT - проекция вектор на единичен вектор допирателна. Стойността на един определя скоростта на степента на промяна на посоката и големината на AT - темп на изменение на скоростта на модула.
Ако има такова движение се нарича униформа. Pria_ движение е ravnoperemennym (в ravnozamedlennym при равномерно ускорена).
Средна ускорение в интервала от време от материал, което трябва да се нарича количество вектор, равен на съотношението:
Когато граница средно ускорение съвпада с мигновен ускорение:
Формула ускорение в различни координатни системи
На декартови координати на проекцията на ускорение (брадва, AY, AZ) на оста (X, Y, Z) могат да бъдат представени като:
където - на единичен вектор от осите X, Y.Z. В този модул ускорение е:
В цилиндрична координатна система, ние имаме:
В сферичната координатна система модул ускорение може да бъде дефинирана като:
Примери за решаване на проблеми
Задача. Материалът се движи по протежение на периферията (фиг.1), която има радиус R = 2m, уравнението на движение, gdetv секунди и S в метри. Това ускорение модул, който посочи т = 3 гр?
Решение. Като основа за решаване на проблема с помощта на формулата:
Използване на предварително определено уравнение на движение, ние получаваме модула на скоростта на материална точка:
Разнообразяване на уравнение (1.2) скоростта на модула по отношение на времето ние получаваме тангенциален компонент на ускорение:
За изчисляването на нормалната компонента на скоростта на материалната точка на нашето движение трябва да се използва израза (1.2), за да се намери:
Използване на израза (1.1) изчисляване на желания ускорението:
Задача. Какво е зависимостта на ускорение на материал точката от време (а (т)), ако се движи на частиците по ос Х и неговата скорост варира в съответствие с уравнението: където - константа по-голяма от нула? При първоначалното време (при Т = 0 и), на материал точка е в основата (х = 0 т). Равен насрочи (т).
Решение. могат да бъдат написани от условията на проблема, че:
Използване формула (2.1), ние откриваме зависимост координатите xot от време (х (т)):
където константата на интеграция може да се намери от първоначалните условия на проблема. Ние знаем, че х (0) = 0, а след това C = 0. В момента има:
Като се използва формулата за намиране uskoreniyadlya нашия случай (движение по оста X):
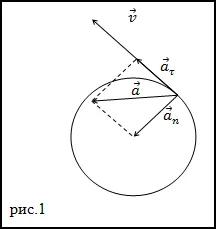
ние се получи желаният експресията за (т):
Отговор. ускорение не зависи от времето, след това насрочи (т) под формата (Фиг.2).