11 семинар

Криви на втори ред в равнината.

фон

I. Уравнението на линия на самолета.

Opredelenie.Uravneniem линия (крива) в равнината

11 семинар
в Декартова координатна система се нарича уравнение
11 семинар
, където
11 семинар
- функция на две променливи
11 семинар
и
11 семинар
. В полярна координатна система, уравнение линия има формата
11 семинар
. Ако уравнението
11 семинар
решими по отношение на променливата
11 семинар
, уравнението на линията може да се запише като
11 семинар
.

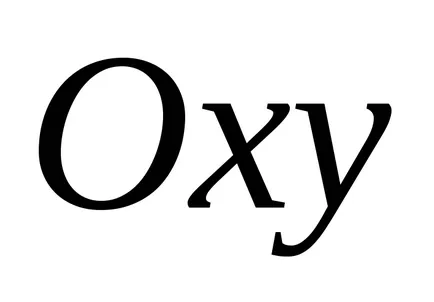
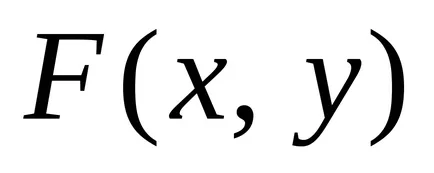
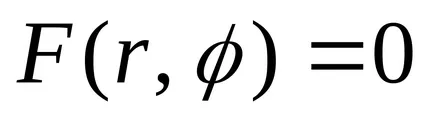
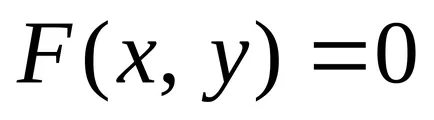
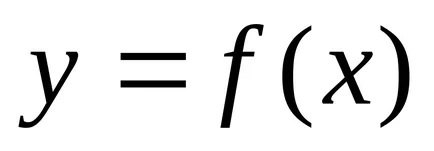
Тъй координатите на точка на линията, свързани чрез уравнението, линията е едномерен геометричен обект. Проблемът с намирането на точките на пресичане на двете линии, дадени от уравненията

11 семинар
и
11 семинар
,

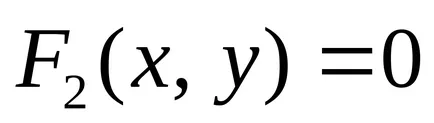
се свежда до решаване на система от две уравнения с две неизвестни:

11 семинар

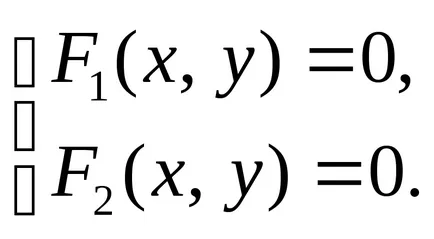
Линия на самолета също може да бъде определен по параметри с помощта на две уравнения

11 семинар

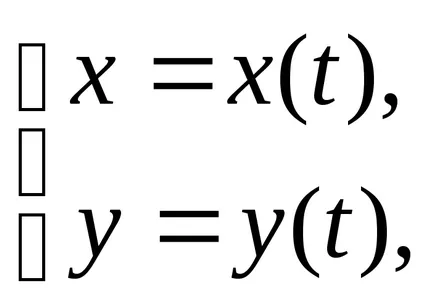
където

11 семинар
и
11 семинар
- координатна точка лежи на линията, и
11 семинар
- променлива nazyvaemayaparametrom.

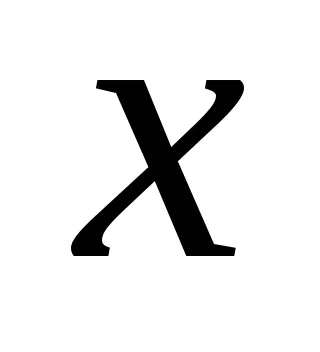
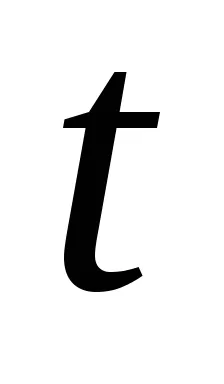
Това са някои примери на линии.

радиусът на кръга

11 семинар
центриран в основата.

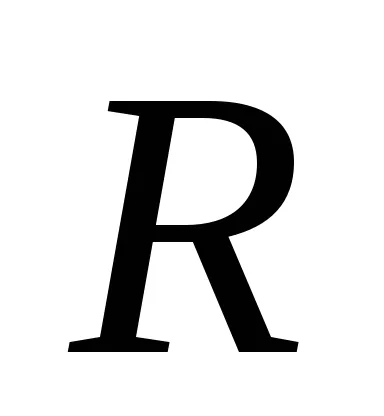
Уравнения такъв кръг имат формата:

а)

11 семинар
- в декартова координатна система;

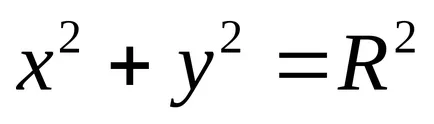
б)

11 семинар
- в полярна координатна система;

в)

11 семинар
- в параметрична форма.

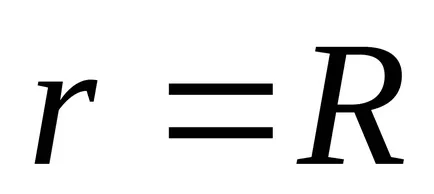
В параметри форма на крайната циклоида уравнение има формата

11 семинар

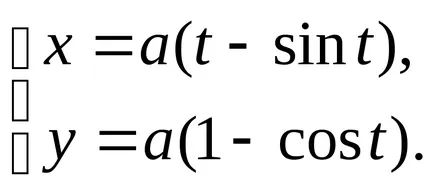
Той описва една точка на кривата на окръжност с радиус

11 семинар
, който се търкаля без плъзгане на фиксираната линия.

Astroid дадено от уравненията:

а)

11 семинар
- в декартова координатна система;

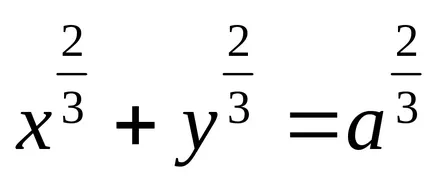
б)

11 семинар
- в параметрична форма.

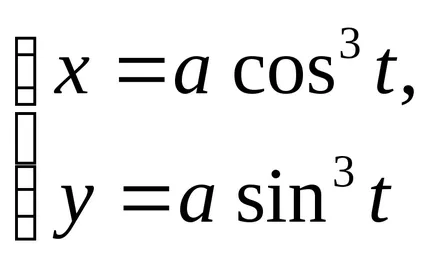
Той описва една точка на кривата на окръжност с радиус

11 семинар
, които ролки без плъзгане на вътрешната страна на окръжност с радиус
11 семинар
.

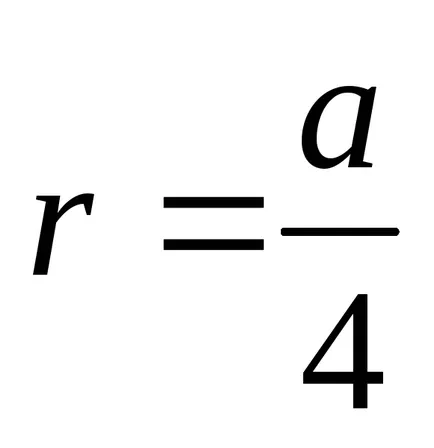
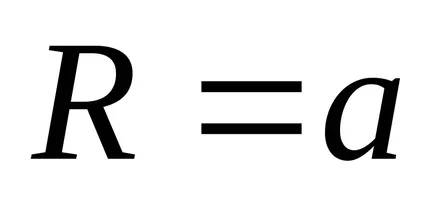
Уравнение кардиоидния полярна координатна система се изчислява по формулата

.

Тази крива описва окръжност с радиус точка

11 семинар
, подвижен по периферията на същия радиус от външната страна.

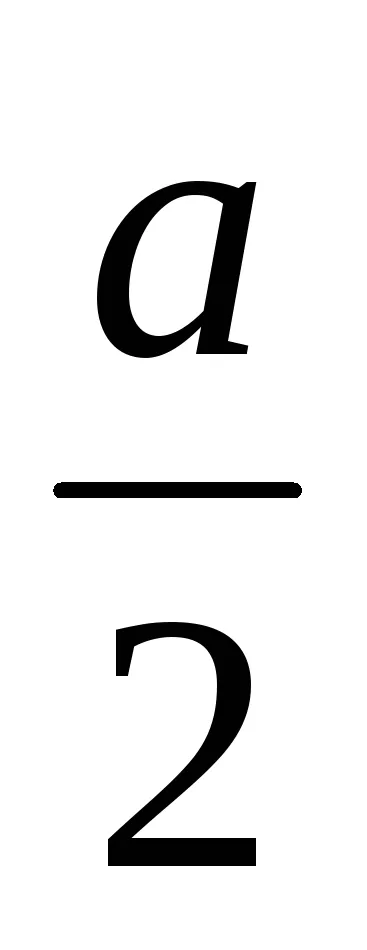
Кардиоидния уравнение е специален случай (

11 семинар
) Охлюви Pascal

.

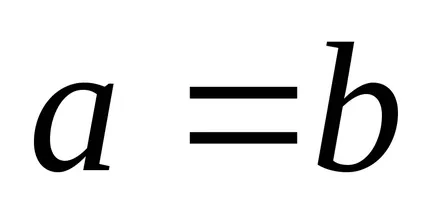
Бернули лемниската дадено от уравненията:

а) - в декартова координатна система;

б)

11 семинар
- в полярна координатна система.

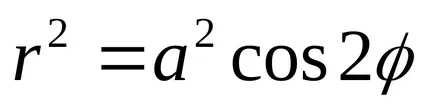
Продуктът на разстоянията от всяка точка лемниската Бернули на две точки от данни

11 семинар
и
11 семинар
е равен на квадрата на разстоянието между точките
11 семинар
и
11 семинар
.

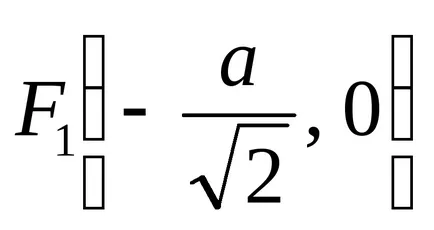
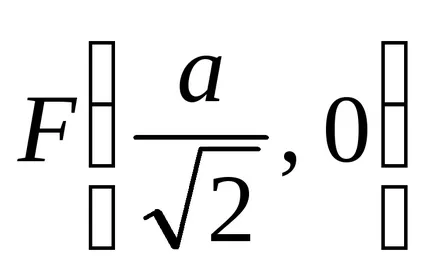
Декартови лист дадено от уравненията:

а) - в декартова координатна система;

б)

11 семинар
- в параметрична форма.

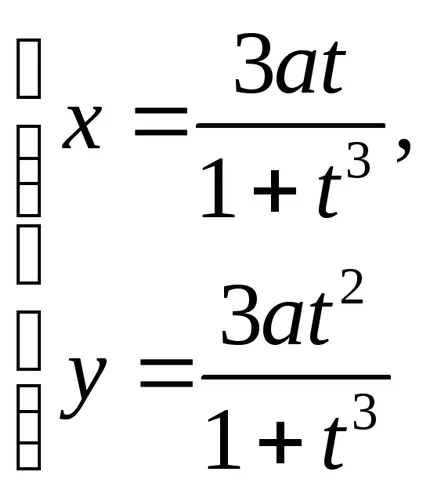
В параметри формата на кривата се дава чрез уравненията

11 семинар

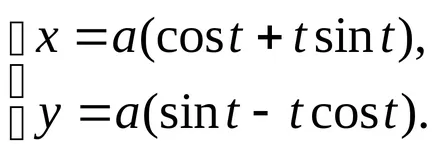
9) нарасна три пъти.

тази крива в полярна координатна система е определена в уравнението

11 семинар

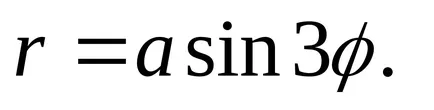
10) chetyrehlepestkovaya роза.

уравнение му има формата

11 семинар
.

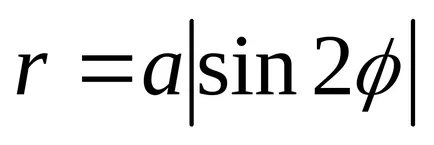
11) спирала на Архимед.

Тази крива в полярен координатна система, описана от уравнението

11 семинар

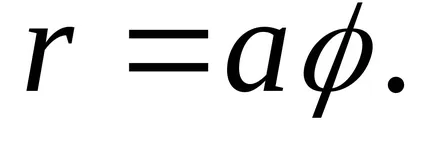
12) логаритмична спирала.

уравнение му има формата

11 семинар

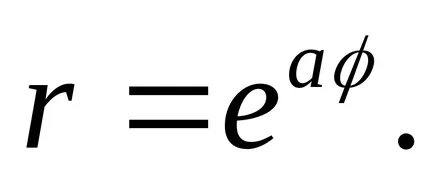
13) хиперболична спирала.

Тази крива се изчислява по формулата уравнения

11 семинар

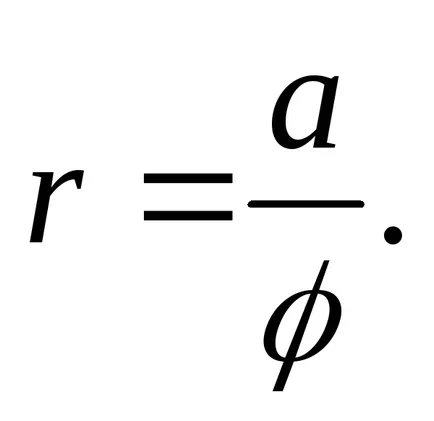
II. Общото уравнение на втория ред и да го доведе до канонична форма.

Общата втори ред уравнението на линията има формата

Предполага се, че

11 семинар
. В този общ вид е трудно да се види как кривата ние се занимаваме с. Следователно разследването на кривата определя от това уравнение, следва първоначално да доведе уравнението помощта на координатна трансформация на каноничен (простата) форма.

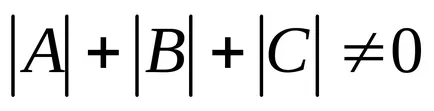
Паралелен превод на произхода.

Нов (грундирани) координатна система, въведена с помощта на отношенията

11 семинар

В новата координатна система, уравнението (1) се превръща

Като се като константи

11 семинар
и
11 семинар
Разтвор на системата

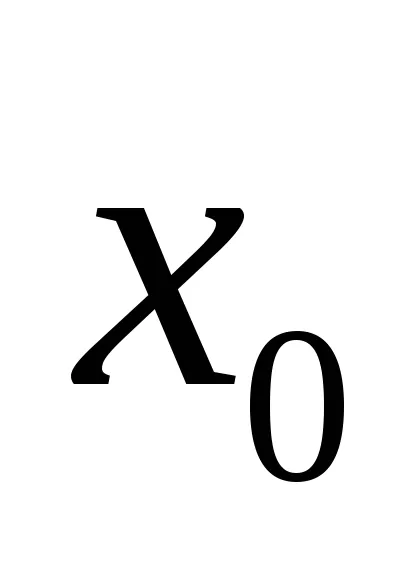
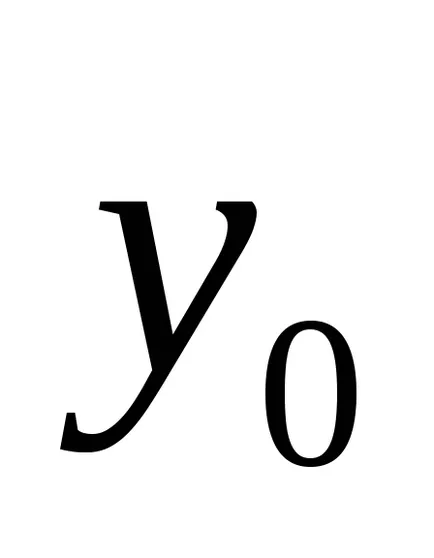
можем да елиминираме от уравнението на кривата с условията на първостепенните променливи

11 семинар
и
11 семинар
. По този начин, в декартова координатна система с новия център
11 семинар
уравнение на втората крива, за да има формата

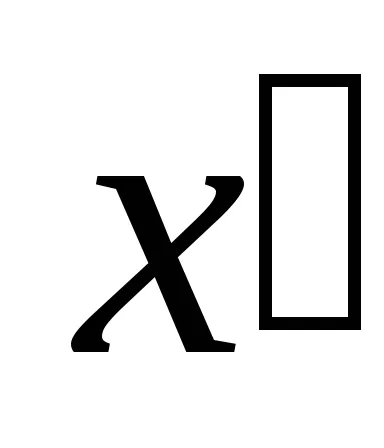
При решаването на системата от уравнения (2) възможни случаи:

1)

11 семинар
. Системата има уникално решение, точката
11 семинар
nazyvaetsyatsentrom крива. а самата крива се нарича централна крива. са в центъра криви

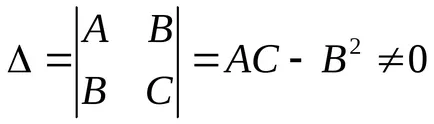
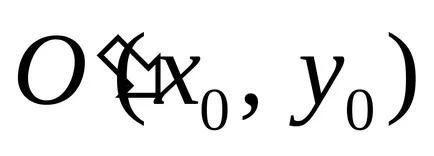
2). Може да има случаи:

а) системата уравнения няма решение, кривите не разполагат с центъра и призова параболи;

б) системата от уравнения има безкраен брой решения, кривата се нарича дегенеративен парабола (или двойка въображаеми успоредни линии на точка).

На следващо място, за разглеждане на делото от криви централни подробности. Ние правим въртенето на координатните оси от ъгъла

11 семинар
около центъра
11 семинар

11 семинар

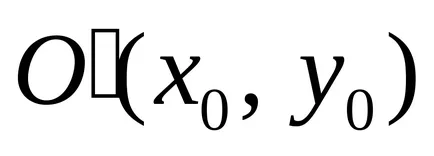
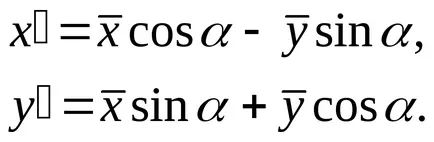
крива на Уравнение (3) става

,

Ние избираме на ъгъла на завъртане на координатните оси

11 семинар
, задоволяване на равенството

11 семинар
или, което е същото, равенство. Този ъгъл на въртене е избран от състоянието
11 семинар
. Следователно уравнението на кривата в координатната система
11 семинар
primetkanonichesky гледания

.

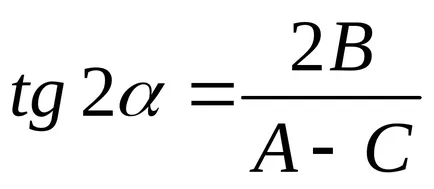
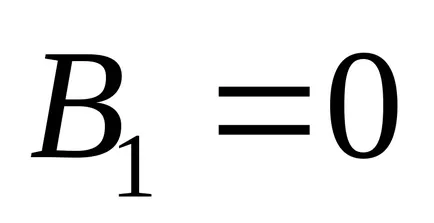
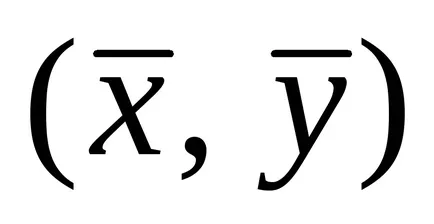
Пример. Нека каноничната форма уравнението на втората крива на поръчката, за която. Намираме координатите на центъра на кривата на системата от уравнения

11 семинар
11 семинар

11 семинар
. В грундирана координатната система уравнение на кривата става

.

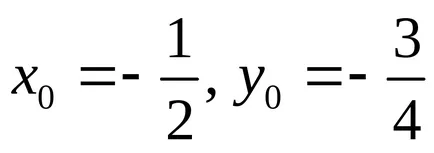
Имайте предвид, че за даденото, т.е. кривата кривата е елипса. Завъртане на координатните оси на ъгъл

11 семинар
, който се намира от уравнението. Това уравнение има две решения. като
11 семинар
, Получените две решения съответстват на две взаимно перпендикулярни посоки. Ето защо, подмяна на един ъгъл на друг води само да замени ос
11 семинар
ос
11 семинар
(Или обратното). Нека разгледаме първото решение
11 семинар
. Като се има предвид, че
11 семинар
и
11 семинар
, ние откриваме
11 семинар
и
11 семинар
, както и коефициентите
11 семинар
и
11 семинар
. Спомнете си, че да се намери на ъгъла на завъртане на координатните оси е равенството
11 семинар
. По този начин, уравнението на кривата в новата координатна система приема формата

11 семинар
.

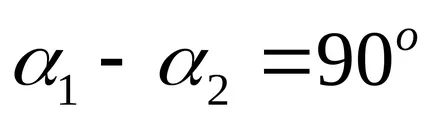
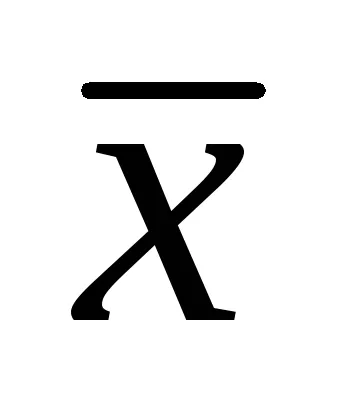
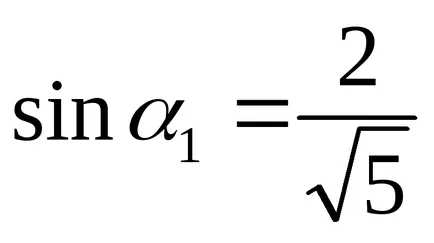
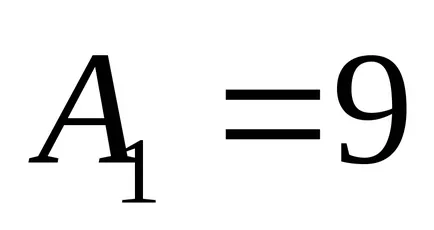
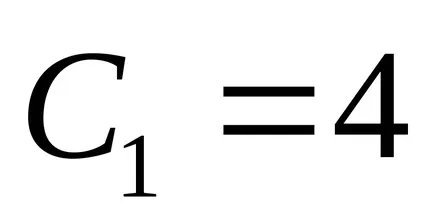
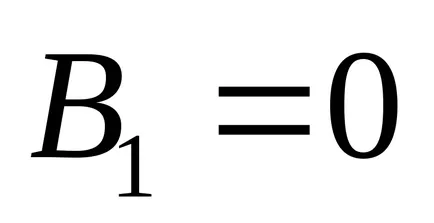
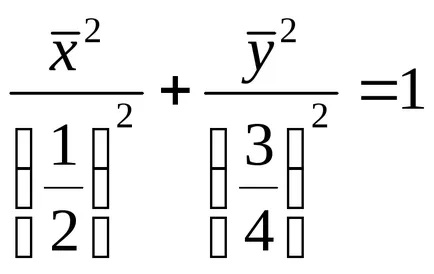
Имаме каноничното уравнение на елипса с полуоси

11 семинар
.