достъпност матрица - studopediya

графика връх се нарича постижима от връх на графиката, ако има най-малко един път от до.

Наборът от върховете R (VI). достъпна от някакъв връх. Тя се изчислява по формулата:

Всъщност, първият елемент в пакета е връх. който е достъпен от самата чрез дължина на пътя нула; G (VI) - набор на върховете VJ. VI постижима от използването на пътищата на дължина он; T 2 (VI), - множество от върховете достъпен от VI като се използва дължина на двата канала; - множество от върховете достъпни от р VI използване дължини път. По този начин, комплект R (VI) се получава чрез последователно извършване на операция на сливане от ляво на дясно в израза (2.9), докато захранващия ток набор не престава да се увеличи при следващата операция сливат. От тази гледна точка за допълнителните операции, няма да дават асоциацията на нови елементи към зададената R (VI). Броят на организации, които трябва да се извърши зависи от графиката Г. Въпреки това, ако графиката е ограничен, а след това р

Достъпност матрица се нарича квадратна матрица за п. кой елемент

Пример. Построява се матрица на достъпност графика G, показано на фиг. 2.6.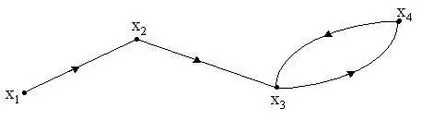

Следователно матрица достъпност има формата:

Очевидно е, че елементите ди, I = 1, т = 1, 2, ..., п, като всеки връх е достъпен от само себе си.

kontrdostizhimostey матрица (обратен достъпен) се определя както следва:

където Q (VI) - набор на върховете VI ÎV., че всеки връх на този комплект може да достигне до върха на VI:

при което - множество от върха, на върха на която се постига с помощта VI единица дължина на пътя; ) - множество от върха, на върха на която се постига VI, като се използва дължина на пътя на две, и т.н. операция на Съюза в израза (2.10), от ляво на дясно, докато друга асоциация вече не се промени "текущия набор".

Пример. Построява матрица Q kontrdostizhimostey за G Фиг. 2.6.

kontrdostizhimostey матрица ще изглежда така:

От дефиницията на матрица D и Q, следва, че Q = D T. Тъй D (VI) е набор от върховете достъпни от. и Q (VJ) - множество от върха, на върха на която се постига VJ. тогава D (VI), - множество от върхове, всяка от които принадлежи към най-малко един път тече от VI до VJ. Тези върхове се наричат основни (незаменими) по отношение на двете крайни вертикали VI и VJ. Върхове се наричат несъществени (прекомерно), тъй като отстраняването им не влияе на пътя от VI до VJ.