Директно в космоса
Литература: Събиране на проблеми в областта на математиката. Част 1. Редактирано от A. V. Ефтимова, BP Demidovich.
Има директни форми на писане на уравнението в пространството:
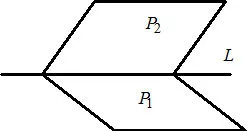
1) $ \ ляво \ A_1x + B_1y + C_1z + D_1 = 0 \ четири (P_1) \\ A_2x + B_2y + C_2z + D_2 = 0 \ четири (P_2) \ край \ полето. - $ общо уравнение на права $ L $ в пространството като линията на пресичане на две равнини $ P_1 $ и $ P_2 $.
-$ Canonical уравнение директно $ L, $, която преминава през точка $ М (x_0, y_0, z_0) $ паралелно вектор $ \ Номера = (т, п, р). $ Vector $ \ Номера S $ е посока вектора на права $ L. $
3) $ \ Frac = \ Frac = \ Frac - $ уравнение на линия, която преминава през две точки $ А (x_1, y_1, z_1) $ и $ B (x_2, y_2, z_2) $.
4) сравняване на всяка от частите на каноничен уравнение 2 до prarametru $ т, $ получи параметри уравнение на линията:
Местоположение на двете линии в пространството.
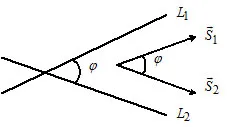
Състоянието на паралелизъм на две линии: Директен $ L_1 $ и $ L_2 $ са успоредни, ако и само ако $ \ overline_1 \ паралелно \ overline_2 \ Leftrightarrow $ $ \ Фрак = \ Фрак = \ Фрак $.Състоянието на перпендикулярност на две прави линии: $ L_1 \ престъпника L_2 \ Leftrightarrow $ $ \ overline_1 \ престъпника \ overline_2 \ Leftrightarrow $ $ \ cdot + \ cdot + p_1 \ cdot p_2 = 0. $
Разстоянието от точка до линията равна на дължината на перпендикуляра от точка на дадена линия.
Нека линия $ L $ е даден от = \ Фрак = \ Фрак $ \ Фрак,Така $ $ \ Номера S = (m, п, р) $ Също нека $ M_2 = (x_2, y_2, z_2) -. $ Произволна точка, принадлежаща на пряка $ L. $ Тогава разстоянието от $ M_1 = (x_1, y_1 , z_1) $ до линия $ L $ могат да бъдат открити от формулата: $$ г (M_1, L) = \ Frac \ Номера S] |> $$.
2.198. Добави каноничната уравнението на линия, минаваща през точка $ M_0 (2, 0, -3) $ паралелно:
а) вектор $ Q (2, 3, 5); $
д) директно $ х = -2 + т, у = 2т, Z = 1 \ fract. $
а) се използва (2) на уравнението на линия в пространството:
$ \ Фрак = \ Фрак = \ Фрак-$ Canonical уравнение директно $ L, $, която преминава през точка $ М (x_0, y_0, z_0) $ паралелно вектор $ \ Номера = (т, п, р). $
Чрез хипотеза $ M_0 (2, 0, -3) $ и $ \ Номера = Q (2, -3,5). $
б) линия, успоредна на дадена линия, той трябва да бъде успоредна на вектор посока. Посока вектор на права $ \ Frac = \ Frac = \ Frac $ има координира $ \ Номера S (5, 2, 1). $ След това намери уравнението на права линия, преминаваща точка $ M_0 (2, 0, -3), успоредна на вектор $ $ \ Номера S (5, 2, 1) $ както в етап а):
а) OX ос е посока вектор $ Аз = (1, 0, 0) $ Така търси линейно уравнение преминаване точка $ M_0 (2, 0, -3), успоредна на вектор $ $ и (1, 0, 0) .: $
г) Директна определя като пресечната точка на две равнини, перпендикулярни на нормалните на двете равнини. следователно посока вектора на права линия
$ \ Ляв \ 3 х-у + 2Z-7 = 0, \\ х + 3Y-2Z-3 = 0; \ Край \ прав. $ Може да се дефинира като кръст продукт на нормален набор от самолети.
За равнина $ P_1: $ $ 3 х-у + 2Z-7 $ 0 = нормално координати вектор има $ N_1 (3, 1, 2); $
за plososti $ P_2: $ $ х + 3Y-2Z-3, $ нормален вектор има координира $ N_2 (1, 3, -2) $.
Намираме вектор продукта:
Така посока вектора на права $ \ ляво \ 3 х-у + 2Z-7 = 0, \\ х + 3Y-2Z-3 = 0; \ Край \ прав. $ Има координати $ \ Номера S (-4, 8, 10). $
След това трябва да се намери уравнението на права линия, преминаваща точка $ M_0 (2, 0, -3), успоредна на вектор $ $ \ Номера S на (-4, 8, 10): $
д) Намери посока вектора на права $ х = -2 + т, у = 2т, Z = 1 \ fract $ Ние напиши уравнението на тази линия на каноничната форма .:
Следователно, ние откриваме посока вектор $ \ Номера S \ ляво на (1, 2, - \ Фрак \ вдясно) $ координатна посока вектор умножете по 2 (за да се отървете от фракции): $ \ Номера S_1 (2, 4, -1) $ ..
След това трябва да се намери уравнението на права линия, преминаваща точка $ M_0 (2, 0, -3), успоредна на вектор $ $ \ Номера S на (2, 4, 1): $
2,199 (А). Добави уравнението на линия, минаваща през двете дадените точки $ M_1 (1, -2, 1) $ и $ M_2 (3, 1, 1). $
Използване на формула (3) в пространството на пряка уравнение:
$ \ Frac = \ Frac = \ Frac - $ уравнение на линия, която преминава през две точки $ А (x_1, y_1, z_1) $ и $ B (x_2, y_2, z_2) $.
Заместването на дадените точки:
2.204. Намерете разстоянието между успоредни линии
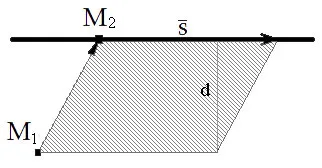
Разстоянието между успоредните линии $ L_1 $ и $ L_2 $ е разстоянието от произволна точка права $ L_1 $ да насочи $ L_2. $ Следователно, може да се намери с формула $$ г (L_1, L_2) = г (M_1, L_2) = \ Фрак, \ Номера S] |>, $$ където $ M_1- $ произволна точка на линията $ L_1, $ $ M_2 - $ произволна точка на линията $ L_2, $ $ \ Номера S - $ посока вектор на прав $ L_2 $.
От каноничните уравнения вземат директно точка $ M_1 = (2, 1, 0) \ в L_1, $ $ M_2 = (7, 1, 3) \ в L_2, $ $ \ Номера S = (3, 4, 2). $
Следователно ние откриваме $ \ Номера = (7-2, 1 - (- 1), 3-0) = (5, 2, 3); $
$ [\ Номера \ Номера S] = \ beginijk \\ \\ 523 342 \ край = I (4-12) -j (10-9) + К (20-6) = $ $ = - 8и-к + 14к. $
За да намерите разстоянието от $ A $ до линията на L $, $, ние трябва да изберете произволна точка $ М, $ принадлежност към директните $ L $ и да намерят посока вектор на линията.
Изберете точка $ $ М. Нека координатите на $ Z = 0. $ Заместването на тази стойност в системата:
Така $ М = (- 14 - \ Frac, 0) $
Намираме вектор посока като вектор продукт на нормалните равнини, определени:
За равнина $ P_1: $ $ 2x-2y + Z + 3 = 0 $ нормален вектор има координира $ N_1 (2, -2, 1); $
за plososti $ P_2: $ $ 3x + 2y + 2Z + 17 = 0, $ нормален вектор има координира $ N_2 (3, -2, 2) $.
Намираме вектор продукта:
Така посока вектора на права $ \ ляво \ 2x-2y + Z + 3 = 0, \\ 3x-2y + 2Z + 17 = 0 \ край \ полето. $
има координати $ \ Номера S (-2, -1, 2). $
Сега ние можем да използваме формула $$ г (A, L) = \ Frac \ Номера S] |.> $$
$ \ Номера = \ наляво (2 - (- 14), 3- \ оставя (- \ Frac \ полето), - 1-0 \ дясно) = \ ляво (16, 15 \ Frac, -1 \ дясно) $
$ [\ Номера \ Номера S] = \ beginijk \\ 1615,5-1 \\ - 2-12 \ край = I (31-1) -j (32-2) + К (-16 + 31) = $ $ = 30i-30J + 15k. $
2.212. Добави каноничната уравнението на линия, която преминава през точка $ M_0 на (3, -2, -4) $ $ успоредна на равнината Р: 3x-2y-3Z-7 = 0 и пресича линията $ $ L: \ Frac = \ Frac = \ Frac . $
равнина P_1 Уравнението $, $, която преминава през точка $ M_0 на (3, -2, -4) успоредно на $ $ 3x-2y-3Z-7 = 0 равнина: $
$ P :. 3x-2y-3Z-7 = 0 \ стрелкаНадясно \ Номера N = (3, -2, -3) $ облагодетелствана равнина преминава през точка $ M_0 на (3, -2, -4) перпендикулярна вектор $ $ \ Номера N (3, -2, -3). $
$ P_1: 3x-9-2y-4-3z-12 = 0 \ стрелкаНадясно $
След това намери точката на пресичане на равнина $ P_1 $ и $ L. $ направо се пише линейно уравнение $ L $ в параметрична форма:
След заместване на стойност $ х, у $ и $ Z, $ изразено чрез $ т $ $ равнина уравнение в P_1, $, и от получената уравнение vyrazm $ T: $
Заместването намери $ т $ стойност може да се настрои по права линия уравнение $ L, $ намерите координатите на пресечните точки:
По този начин, директно $ L $ и $ P_1 $ равнина пресичат в точка $ M_1 (8, -8, 5). $
Сега напишете уравнението на линията, минаваща през точките $ M_0 $ и $ M_1 (8, -8, 5) $ (3, -2, -4.) - това ще бъде най-желаната линия. Ние използваме формула (3) $ \ Frac = \ Frac = \ Frac: $
б) Добави уравнението на линия, минаваща през двете дадените точки $ M_1 (3, 1, 0) и $ $ M_2 (1, 0, -3). $
2.206. Докаже, че линиите $ L_1: \ ляво \ 2х + 2y-Z-10 = 0, \\ край XYZ-22 = 0, \ \ полето $ и $ L_2: .. \ Frac = \ Frac = \ Frac $ паралелно и намерите разстояние $ \ Ро (L_1, L_2) $
2.207. Създаване уравнение права линия, минаваща през $ х-3Y + 2Z пресечните точки на равнината 0 + 1 = $ права $ \ Frac = \ Frac = \ Frac $ и $ \ Frac = \ Frac = \ Frac. $
2.211. Добави уравнението на линия, минаваща през точка $ M_0 (7, 1, 0) равнина, успоредна $ $ 2х + 3Y-Z-15 = $ 0 и пресичаща линия $ \ Frac = \ Frac = \ Frac $.