0 кръг на Аполоний

0.6. Аполоний кръг

Да разгледаме проблема с намирането на мястото на точки в равнината, съотношението на разстоянията от което двете точки от данни - константа. За да се реши този проблем ние използваме метода на координати, а именно ние получаваме форми на уравнение, образувани от мястото, и след това проучване неговите геометрични свойства.

Представяме правоъгълна координатна система, избиране като нейното начало една от две дадени точки А и В (например, В), а оста Ox - така че втората точка (нека това да бъде точка А), разположена на положителен половина (виж Фигура 10.6 .. 0.1).

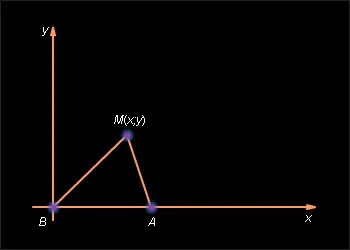
В тази координатна система, точка В има координатите (0, 0) и точка А - (с 0), където> 0. Да М (. Х у) - произволна точка, отговаряща на състояние на проблема, т.е. AM = к · BM. където к - дал положително число. Ако к = 1, това означава, че желания набор се състои от точки на еднакво разстояние от информационни точки А и Б. Свойствата на перпендикулярна на сегмента, следва, че желания набор в този случай е права линия, минаваща през средата на перпендикуляра на сегмента AB ОХ ос. Сега нека к ≠ 1. От Теорема 10.2 имаме и състоянието на точката M доставя желаното комплект може да се запише като

Това уравнение е еквивалентно на равенства

Отделяйки точен квадрат, получаваме

Това уравнение на окръжност с център в точката лежи на говедото на ос. и радиуса

Получената кръга носи името на древногръцкия Geometer Аполоний. реши да възложи на чисто геометрична метод.
страница 1

0 кръг на Аполоний
16.36kb. 1 р.

Ellipse Tool и задръжте клавиша Ctrl, начертайте два кръга, единият от които с диаметър малко по-голям от последния. По-малък кръг се попълва помощта на функцията Fointain Напълнете
15.18kb. 1 р.