Задачи за независим решение
Производно на функция и нейните приложения
Увеличаване на аргумента и нарастването на функцията
Като се има предвид функция. Fix някаква стойност. Нека дадем произволна променлива увеличение. На мястото, функцията ще бъде създадена. Разликата между новата стойност на функцията и старата си стойност, наречена нарастването на функцията и е обозначен. По този начин, нарастване на функцията е стойността
.
Да. след това. намерени:
=.
2.2. Концепцията на производно.
Да - произволна функция повторно променлива х. Ние се определи стойност на аргумента х и изчисляване на съответната стойност на функцията. Нека дадем нарастването на аргумента. Има нов ценности-сет се изчислява съответното нарастване на функцията. изготвят нагласа
и разгледа граница
.
Това ограничение се нарича производно с функция у = F (х) на х и у е означен ". u'x. F '(х) или по-малко. По този начин, производно се нарича граница на увеличените съотношение функция-на нарастване на аргумента, където стъпката на аргумент клони към нула.
Действието на намиране на производна на функция се нарича по-разграничаване на тази функция.
Геометрична смисъла на производното
Да приемем, че функция у = F (х) има производно в точка x0. След графика на функцията в точката на M0 (x0. Y0) може да се направи допирателната, уравнението е от формата
,
В това уравнение = TGA - когато - ъгъл на наклона на допирателната към оста х.
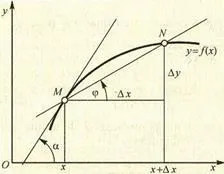
Така геометрично производно е наклонът на допирателната към крива-нето на мястото счита.
Физическата смисъла на производното
Нека се движи точка по права линия, така че - пътят пресича от точката, в момента тон. След пътя пресича от точката в интервал Dt време от тона на време Т + DT. е DS = F (т + Dt) -f (т). В този случай,
е средната скорост на точката в интервала от време от Т в Т + Dt.
скорост точка в този момент е границата на средната скорост по време на интервал от време Dt. т.е.
(1.2) и определянето на производно (1.1) следва, че. т.е. производно на пътя по отношение на времето в праволинейно движение е скоростта.
Правила за изчисляване на производни
Следните формули експресират правила проводими количество на диференциация, продукт, коефициент функции, и изчисляване на производно на постоянна стойност.
1) производно на постоянна величина, равна на нула:
2) Размерът производно равна на сумата на производни:
.
.
3) производно продукт:
.
.
4) константа може да се приема като знак на производното:
.
Това правило е следствие на правилата 1), както и в областта на върховенството 3).
.
5). Производни Private:
.
Тук се приема, че смята стойността на знаменателя не е нула.
=
=.