задачи B9

Ние продължаваме урок №8 изпит по математика.
Днес, ние се нуждаем от следната таблица за решаване на проблемите. показваща връзката на знака производно с функция монотонна.
Моля, бъдете изключително внимателни в следващия. Вижте насрочи КАКВО дава на вас! Функция или негово производно
Ако даден графиката на производно. че интересът ни са само признаци на функциите и нули. Не "хълмове" и "депресия" не ни интересуват по принцип!
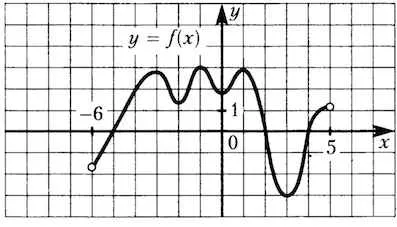
Фигурата показва диаграма на функция, определена на интервал. Определя се броят на решетка точки в което производното е отрицателен.
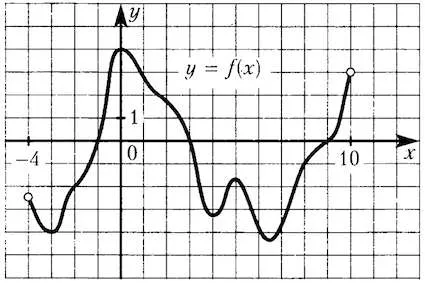
На фигурата са откроени намаляване площ функция:
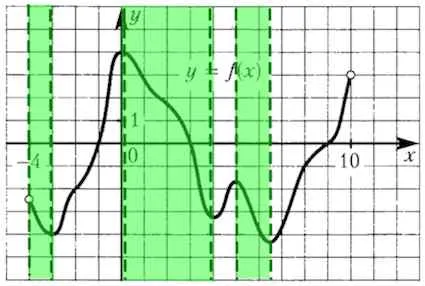
В тези области на намаляване на функцията попада 4 целочислени стойности.
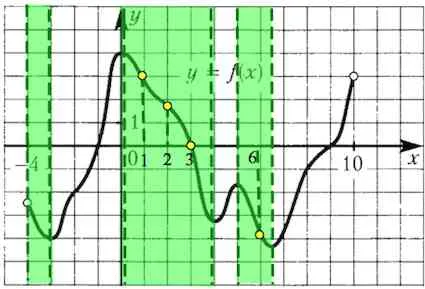
Фигурата показва диаграма на функция, определена на интервал. Намерете броя на точките, в които допирателната към графиката на паралелен прав или съвпада с него.
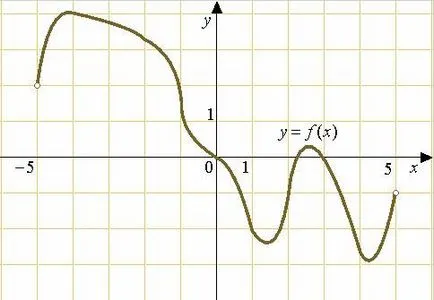
След допирателната към графиката на паралелно (или съвпада с) линията (или, еквивалентно,) с наклон равен на нула, и наклона на допирателната има.
Това от своя страна означава, че допирателната е успоредна на оста, тъй като наклонът е наклонът на допирателната на оста.
Следователно, ние откриваме, в точката на диаграма екстремум (максимум и минимум точки), - при което допирателната към графиката на функцията да бъде успоредна на оста.
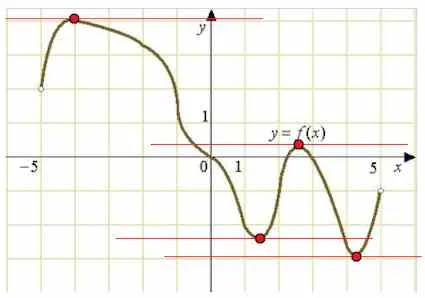
Фигурата показва графика на функцията производно определено на интервала. Намерете броя на точките, в които допирателната към графиката на паралелен прав или съвпада с него.
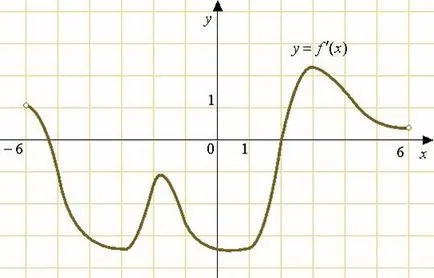
След допирателната към графиката на паралелно (или мач) права линия с наклон, и наклона на допирателната има.
Това от своя страна означава, че точките на контакт.
Затова гледай колко точки на графиката са ординатата равни.
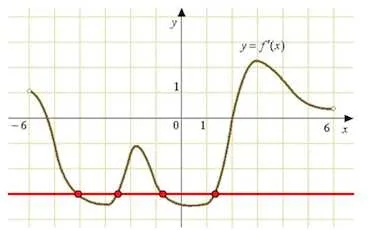
Както можете да видите, тези точки - на четири.
Фигурата показва диаграма на функция, определена на интервал. Намерете броя на точките, в които производната е 0.
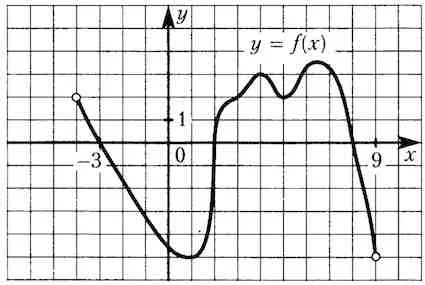
Производното е нула в точки екстремум. Ние ги имаме 4:
Фигурата изобразява графика на функцията и единадесет точки на оста х. В колко от тези точки на производната на отрицателна?
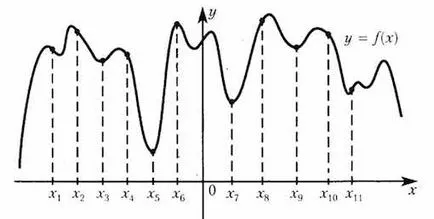
На интервали от намаляване на неговата функция производно е отрицателен. Отслабване на функцията точки. 4 такива точки.
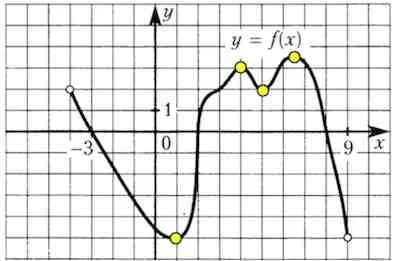
Фигурата показва диаграма на функция, определена на интервал. Намерете сбора на точките на екстремни функции.
Точки екстремум - максимална точка е (-3, 1, 1) и минималната точка (-2, 0, 3).
Сума екстремум точки: -3-1 + 1-2 + 0 + 3 = -2.
Фигурата показва графика на функцията производно определено на интервала. Намерете интервалите на нарастване функция. В отговор, да определи размера на решетка точки, включени в тези интервали.

Фигурата маркирани места, на които производно е положителен.
На малки разликата увеличава решетка точки там, разликата увеличава четири цели числа, и.
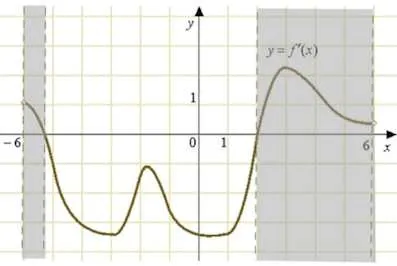
Фигурата показва графика на функцията производно определено на интервала. Намерете интервалите на нарастване функция. В отговора си дължина от най-дългата от тях.
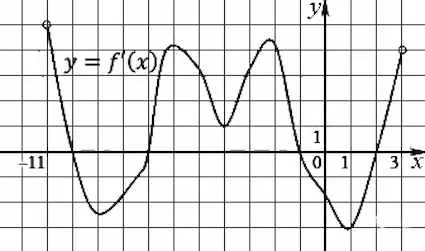
На фигурата са подчертани всички пространства, в който производно е положителен и следователно се увеличава функцията в тези интервали.
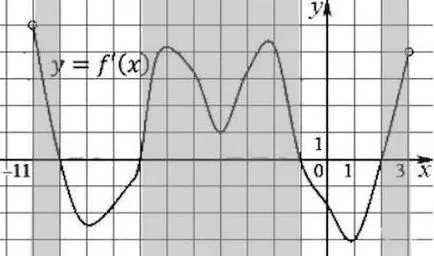
Дължина на най-дългата от тях - 6.
Фигурата показва графика на функцията производно. определена на интервал. В един момент в интервала е най-голямата стойност.
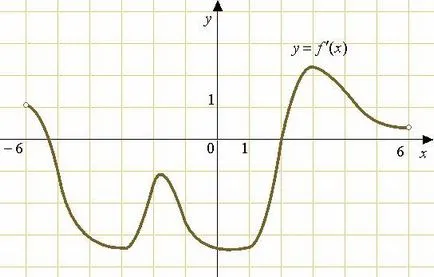
Гледайте поведението на графиката на интервала, а именно, ние се интересуваме от само знака на производната.
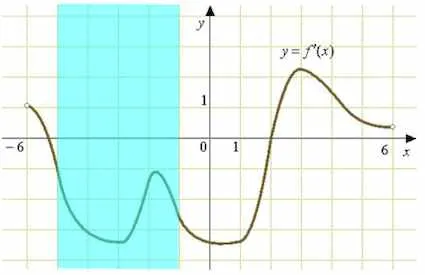
Знакът на производно на - отрицателен, като графика на този сегмент под оста.
Това означава намаляване на функцията на интервала.
Така че, най-важната функция се в началото на отсечката, която е най-важното.
Задача 10.
Фигурата показва графика - функция производно определено на интервала. Намерете броя на максимален брой точки на функцията в интервала.
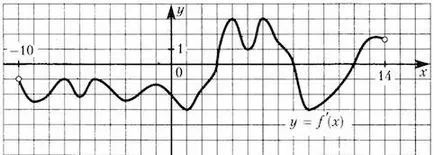
Фигурата показва графиката на производната, така че ние трябва да разбера тази воля интерес само знаците и нули на деривата.
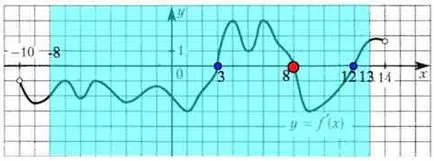
Ние виждаме на снимката в определен интервал () три нули от. Освен това, производното mnyaet подпише при преминаване през него. Това е точката на екстремни функции (максимум и минимум точки).
Когато деривати промени знак "+" в "-" в точката 8, обозначен в червено, и "-" до "+" в две точки (3 и 12), маркирани в синьо.
Така че, когато преминават през максималната точка на функцията промени за увеличаване на спад, и следователно производните промени подписват от "+", за да "-".
Така че, в момента на максималния един (маркирани в червено).
Задача 11.
Фигурата показва графика на функцията и точката маркиран -3, 1, 6, 8. В някои от тези точки е най-малката стойност на производното? В отговор, посочете тази точка.
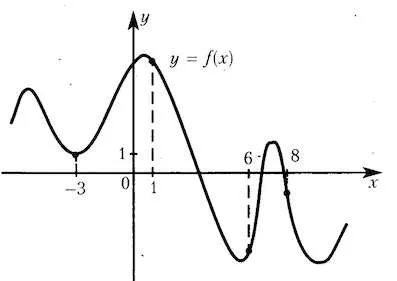
Стойността на производното в точката на контакт е равен на наклона на допирателната. На свой ред, наклонът на допирателната е равен на наклона на допирателната към оста.
В точка 3 (минималната точка), производното е нула.
В точка 6 производното е положително, тъй като точките лежат върху повишаване функцията интервал.
Но в точки 1 и 8 на деривата е отрицателна.
На този етап 8 в тангенциален ъгъл на наклона е ясно по-малък, отколкото в точка 1.
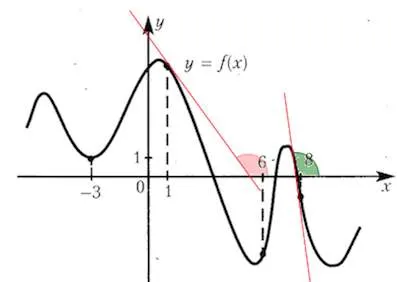
Следователно, в точка 8, наклонът ще бъде най-малките и по този начин стойността на производно ще бъде най-малката.
) Това е време да се отпуснете малко. Не е ли? -> + шоу
Не беше лесно.
Тези момчета вероятно не са прекалено сладки ... Не се отказвайте!


Добър вечер! Аз имам един въпрос, също на деривата, но притесненията и спектри изпъкналост / вдлъбнатина. Защо у функция = х ^ 4 / (X ^ 3 + 1), критичната точка на втория вид на част в интервал вдлъбнатина, това е критична точка в своето второ производно е равно на 0, и необходими съгласно теоремата вземат само интервали където втората производна по-голяма от нула. Благодаря предварително за отговора
Галина, както аз го разбирам, ние трябва да се прави разлика между строга и не-строг изпъкналост / вдлъбнатината на ...
Елена, благодаря за отговора, по погрешка грешна функция, въведени. Всъщност въпросът ми е следният: Аз съм учител и аз съм се интересуват от това как математическа грамотност моите студенти първокурсници обясни вдлъбнатина изпъкналост за функция Y = х ^ 4, защото там е критична точка от втория вид 0, въз основа на които те обясняват, че функцията на своя домейн изпъкнала надолу, 0 спънка. Благодаря.
В задача 2 отговорът не е 3? Наклонът е равно на 0, тогава у = 0 пресича функция в три точки.
Даша, ако графиката на функцията F '(х) (а не е (х)) е показано на фигурата, тогава аргументите ви ще бъде вярна.
Сравнете задачи 2 и 3.
За указания 7 - Защо е х = не включват точка 2? След - "Ако функцията е непрекъсната върху интервала [а, Ь] и увеличава (намалява) в интервала (А; б), се увеличава (намалява) и интервала [а, Ь]"
Site А. Larin EgeTrener - О. Sebedash математика лесно! CSE? Добре! - J. Feldman
