Задача 3 строителни логаритмични честотни характеристики и APFC Hodograph

Съгласно условията на проблема за прехвърляне функция на дадена автоматична система за контрол на линейни е както следва:

2. Изграждане полярен парцел APFC W (й ω) дава ACS.

Пример. Намираме израз за логаритмична честота и фаза отговор, който първо се определи APFC система за нейното прехвърляне функция W (р), на мястото го р Лаплас оператор за комплексна променлива й со.

където: H (ω) = - амплитуда честота характеристика (AFC) система ACS;

φ (ω) = [- 90 + arctg (ω ∙ Т1) - arctg (ω ∙ Т2) - arctg (ω ∙ Т3)] - аргумент на функцията за трансфер на честота, която е въведено честота характеристика (PFC) ACS система.

От известно експресията на честотната ние определяме LACHH L (ω):

Асимптотичната LACHH конструкт чрез замяна на непрекъсната крива LACHH няколко правите участъци, които го правят един с друг в точки, съответстващи на ъгловата честота ωs на (ъгъл честота), което е числено равно на реципрочната стойност на времеконстантата появява в израза (14). В нашия пример имаме три чифтосване честота:

Подредете чифтосване честоти във възходящ ред следните първоначални данни на нашия пример: К = 10; Т1 = 0.4 S; Т2 = 2 S; Т3 = 0.02 с.

Като се има предвид, че по-голяма от стойността на времето константа, по-малка е стойността на честотата на ъгъл, можем да напишем следното неравенство:

Чрез определяне на числовите стойности на ъгловата честота от 0,1 до 100 рад / сек (ωs2

Тъй като стойността на модула на H (ω) APFC обратно с ъгловата честота, е необходимо да се вземат по-висока честота близките стойности относително нисък модул за изграждане на място. Например, в този пример, честота в обхвата от 1 до 10 рад / сек.

Отложи отрицателен реален оста на комплекс равнина стойност N (ω) от проекция модул H (ω) на и за отрицателен реален ос - проекция стойност М (ω) на модула, като преди най-удобно мащаб. След това, през точката на отложено поведение вертикални или хоризонтални линии, успоредни на обратното координатни оси. Чрез свързване на точките на пресичане на тези линии с произхода, ние получаваме вектори APFC съответстващи на честотите, при която изчислената проекция на модула на координатните оси. Чрез свързване на точките на пресичане на тези линии една с друга и с произход, ние се получи фрагмент локус APFC представлява крива, която описва края на вектор W (й со), докато промяна на честотата в избрания честотен обхват.

Друг метод за конструиране APFC локус основава на използването на полярните координати, които на комплекса равнина през началото на координатите се извършват редица линии под ъгъл, взети от таблицата. 4 за съответните честоти, и лежеше на тези линии в произволна скала от стойности на модула на H (ω) APFC. След свързване на краищата на векторите между себе си и произход, ние се получи желаният фрагмент локус APFC.

Фрагмент APFC локус изградени въз основа на таблицата с данни. 4, показано на фиг. 2.

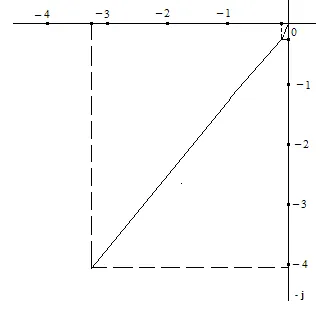
Фиг. Фрагмент 2 локус APFC

За да се построи LACHH, LFCHH и локус APFC да използвате програмата Matlab. Пример фрагмент локус APFC конструира при използване на тази програма е показана на Фиг. 3 за диапазон от честоти 1-15 рад / сек.

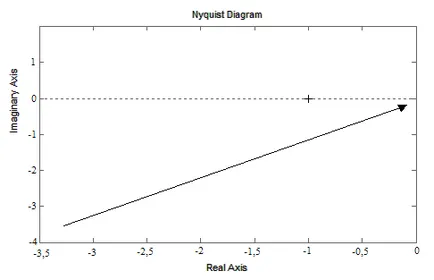
Фиг. 3 Подробности локус APFC конструиран

използвайки Matlab програма

Задачи и указания за прилагане

лабораторна работа брой 1-3

Lab № 1. Изследване на времето и честотата характеристики на линеен ACS.

2. Lab номер 2. Изследване на стабилността на линейна система за автоматично управление.

3. Lab номер 3. качествени показатели Изследвания линейни ACS.

Приложение 1 Кратко ръководство за прилагане на MATLAB система и SIMULINK.

Lab № 1