Вмъкването на сортиране - studopediya
Сортиране вложки (сортиране чрез вмъкване) - прост алгоритъм за сортиране, в която се добавя още един елемент винаги в края на списъка и след това се премества в горната част на списъка, стига да е по-малък от предходния елемент.
По този начин, формално, това е правилното място, където да поставите (например сортиране карти в библиотеката). Този алгоритъм ще има следната последователност от стъпки.
1. Етапът на инициализация. На елемент от масива вече сортирани по възходящ и служи като първоначален списък.
2. Етап итерация. За всички следващи елементи на втората до п -1, следващият елемент и се сравнява с всички предишни елементи от 0 до (I-1), докато текущия елемент и е по-малко от или равно на предишната. След това се открива позиция, за да вмъкнете или ще бъде постигнато начело на списъка. След това, елемент се вмъква в установено положение.
Да предположим, че се дават следния масив:
Анализът на изчислителната сложност показва, че във всеки случай е необходимо за получаване на (п-1) подаване. Във всяка от тези пасажи в най-добрия случай, когато масивът е сортиран във възходящ ред, се изисква едно сравнение. В този случай, пермутацията не е, а цената ще бъде изчислителни
.
В най-лошия случай, когато масива се сортират в низходящ ред за всеки от (п-1) и преминава необходимите сравнения с предишните елементи. Изчислителната сложност е пропорционална. Като цяло, всеки пропуск ще изисква по-малко от половината. Ето защо, средно. Изчислителната сложност все още е пропорционална.
А блокова схема на алгоритъм за сортиране вложки има формата:
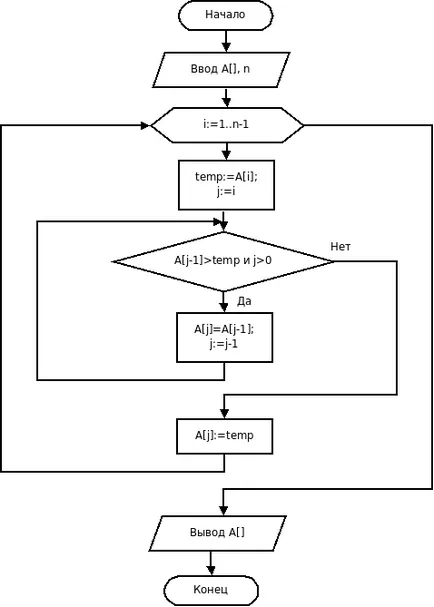
Прилагане на този алгоритъм на C ++, както следва:
невалидни InsertSort (T * A, конст Int п)
а (к> 0 Темп Quicksort алгоритъм (Quick Sort). развит английски информатика Чарлз Хоаре, и е най-бързият в момента сред всички други видове сортове. Тя се основава на едно уникално взаимодействие между двата индекса ScanUp и ScanDown. и може да бъде описан, както следва: 1. Етапът на инициализация. Входът на алгоритъма и предава елемент масив от първите кодове (ниски) и края (високо). След това е индексът, който се намира в средата на списъка. След това, на първия и средния елемент са разменени. По този начин средната елемент се намира в нулево положение и се сравнява с всички други елементи с индекси (ниски 1) до висока. ScanUp индекс минава целия списък и спря, ако се установи, повече елементи от средата (първо ScanUp = ниско 1). списък ScanDown индекс ще тече от края към началото, докато стигнете до елемент на по-малка или равна на средната елемент. Първоначално тя се определя в края на списъка. 2. Етап итерация. За всички елементи, тъй като ScanUp позиция до края, ScanUp се увеличи с 1, докато намери елемент, който е по-голяма от средната елемент или до достигане на края на списъка. Така ScanUp ще посочим елемент, който не е в подсписък, т.е. всички елементи ScanUp да бъде по-малка или равна на средата. След ScanDown индекс е намалял с 1, докато намери елемент по-малко или равно на средата, или до началото на списъка е достигната (ScanDown 3. Изходен етап. стъпка итерация се извършва толкова дълго, колкото е по-малко от ScanDown ScanUp. Това означава, че целият списък е разделен на две части, със стойности, по-малка или равна на средната елемент и със стойности, по-голяма медиалния член. Те споделиха индекс позицията ScanDown. След това средата елемент в нулево положение и елемента с индекс ScanDown възли. 4. Етап рекурсия. Етапи 1-3 се повтарят за лявата под списъка с елементи от ниско до ScanDown -1 и дясно - от ScanDown 1 до високо, докато списъкът не остават празни или сек. Нека оригиналния масив има следния вид: