Вълни в еластична медии
Представете вълна на повърхността на водата под формата на един или гърбица солитонна, Фиг. 9, посадъчен в определена посока. метод на Фурие е сложно -
Noe колебание може да се разлага в група чисто хармонични трептения. Ако всички хармонични трептения се разпространяват над водната повърхност със същите темпове, по -
tyami, а след това със същата скорост ще се прилага, и те образуват комплекс вибрации -
от. Но, ако някои косинус вълна скорости са различни, постоянно променяща се фаза разликата между тях, както и гърбица, в резултат на добавянето им, непрекъснато променя формата си и се премества със скорост, която не съвпада със скоростта фаза на условията аудио вълни.
Всеки сегмент от косинус вълна, фиг. 10, също може от теорема на Фурие разлага на безброй неограничено във времето идеален косинус. По този начин, всеки недвижими вълна е суперпозиция на # 150; група # 150; косинус безкрайна, и неговата скорост на размножаване в диспергиране среда е различна от скоростта фаза на вълни условия. Тази скорост разпространение на реалните вълни в разпространена -
подходяща среда, и се нарича скоростта на група. Само в среда, лишена от дисперсия, истинската вълна се разпространява със скорост, която съответства на скоростта фаза на вълната на косинус, добавяне на които тя се формира.
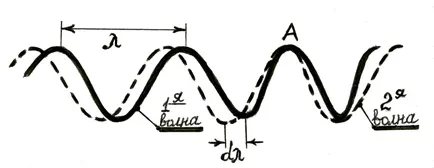

Определяне на експресията на скоростта на група
Да предположим, че една група от вълни се състои от две вълни, малко по-различни по дължина:
а) вълна с дължина на вълната. посадъчен при скорости;
б) дължина на вълната на дължина на вълната. посадъчен със скорост
Относителното позициониране на двете вълни за определен момент от време е показана на Фиг. 11. а. Гърбици две вълни се събират в една точка; на едно място е максимумът на получените трептения. Да. След втората вълна изпреварва първия. След определен период от време, тя ще го изпревари в сегмента; в резултат на което на гърбицата на двете вълни са вече формират на мястото. Фиг. 11. б. т. е. поставят максимално колебанията на получения комплекс ще се премести обратно в интервал равни. Следователно, максималната скорост на размножаване на получените колебания по отношение на средата е по-малка от първата скорост на разпространение на вълната по размер. Тази максимална размножаване колебания скорост комплекс е скоростта на група; това, обозначаващ чрез имаме
Тъй като скоростта на втората вълна спрямо първото равни. на
Сега замени (37) в последния формула и ние се
Ние прилагаме този израз в (38) намираме за скоростта на група
От (39) става ясно, че скоростта на група се различава от по-висока скорост фаза. толкова повече. т. е. по-изразена зависимост от скоростта на разпространение на вълните на тяхната дължина, наречен дисперсия.
Когато скоростта на група. и когато имаме. Следователно скоростта на група може да бъде на по-малко и по-голяма от скоростта фаза.
Скоростта на група е по-малко от фазата, когато. . Т.е., когато по-дългите вълни пътуват доста по-кратки .; Този случай се нарича нормална дисперсия;
За среда, лишена от дисперсия и. т. е. група и фазовите скорости съвпадат.
Ако. късата дължина на вълната надмине вече; Този случай се нарича аномална дисперсия.
- Принципът на суперпозиция на вълни
В размножаване среда в няколко малки амплитуда вълни чрез извършване -
etsya отвори Леонардо да # 150; Vinci, принципът на наслагване: трептене на всяка частица на средата се определя като сумата от независими трептения, които биха се ангажират тези частици по време на размножаване на всяка вълна отделно. Принципът на суперпозиция се нарушава само за вълни с много голям амплитуда, например, в нелинейна оптика. Вълните се характеризират с еднаква и постоянна честота, независимо от време, фаза разлика се нарича последователен; такъв като, например, kosinusoidal -
Най или синусоидална вълна с една и съща честота.
Наречен интерферентни вълни съгласуван Освен това, в резултат на което стабилна трептене печалба във времето на някои места и да го отслаби и в други. По този начин има преразпределение на вибрации енергия между съседни региони на средата. Смущения на вълни се случи, само ако те са последователни.
Специфичен пример за резултат от интерференция между две вълни са толкова
наречен постоянна вълна в резултат на наслагването на две противоположни плоски вълни с еднакви амплитуди.
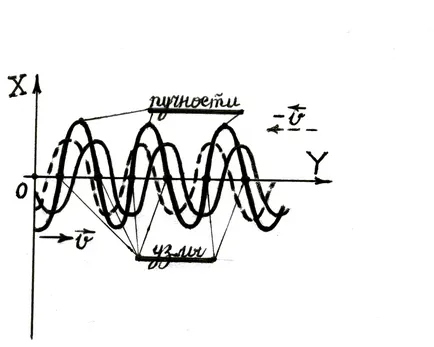
Добавянето на две вълни посадъчен в противоположни посоки
Да предположим, че две плоски вълни с еднаква амплитуди Разпространение -
nyayutsya # 150; Един от положителния пример -
откриване. Фиг. 12, а другият # 150; Погледнато от отрицателната -
Ако произходът се възползвам от тази точка -
.. Ke, на counterpropagating вълни, които имат една и съща посока на преместване, т.е., да имат една и съща фаза, и изберете времето така, че първоначалните фази на око -
, за да бъде равна на нула, а след това уравнение kazh -
Дой плоска вълна може да се запише като:
а) за вълна (8), простираща се към поло -
а) за вълна (8), простираща се в посока на оста положителен
б) за вълна (9) и посадъчен към отрицателната посока.
където - амплитудата на хармонична вълна или амплитудата на вибрациите в тази вълна.
Добавянето на тези две вълни дава
от разкриване на стойността на косинус на сложните аргументи и да правят съкращения, ние имаме
В (40), фактор, показва, че точките на средата настъпва колебание със същата честота. че колебанията на противоположни вълни.
Модификатор. независима от време, той изразява амплитудата
Получената колебания; по-точно # 150; амплитуда като положителна стойност по същество по дефиниция, равна на абсолютната стойност на този фактор:
По този начин, амплитудата на колебанията зависи от координатите. за определяне на позицията на средните точки на.
Получената колебанията (40) се нарича постоянна вълна.
В определени точки на амплитудата на стояща вълна е равна на сумата от амплитудите на двата термина, такива точки се наричат antinodes;
другаде получената амплитуда е нула, тези точки се наричат постоянните възли вълни.
Амплитудата определя от (41) е максимум при точките за който
Следователно позицията на antinodes определено състояние
Следователно, координатите са antinodes
Разстоянието между съседни antinodes се получи, като се използва (42)
т. е. разстоянието между съседните antinodes е равна на половината от дължината на вълните, интерференцията, която се образува тази постоянна вълна.
Амплитудата на получените трептене възли е равно на нула, тук (41) на състоянието на образуване на възли:
Следователно, координатите на възли са
Това означава, че разстоянието от най-близкия възел е равен на antinode
т. е. възли и antinodes са раздалечени от една четвърт дължина на вълната.
Тъй като в този момент е фактор във всички точки на същата стойност, всички точки между два възела осцилира в една и съща фаза, т.е.. Е. Те едновременно достигне максималните отклонения едновременно преминават през позиция на равновесие, и така нататък. Г. точки на двете страни на една и съща възлова точка, осцилира в противоположни фази, т.е.. напр. едновременно достигат екстремни но противоположни по знак на тестваните едновременно равновесие позиция премествания, но с противоположно насочени скорости и т. г.
Averroism - философски и богословски посока в Zap.-европейската философия на Средновековието и Ренесанса, въз основа на арабските гледки. философ Авероес (Авероес). Averroism разработен материалистични тенденции aristotelizma- представа за вечността (оттук и несътворена) свят.