Вектори и матрици
Вектори и матрици.
С подредена последователност от реални числа, А1, А2, .... Може да се свързват асоцииран концепция вектор в п-тримерно пространство и определен като:
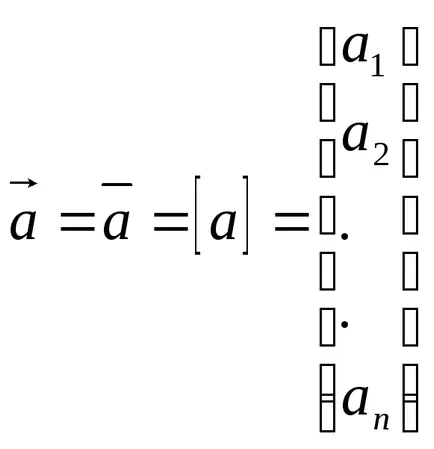
Видове и характеристики на вектори.
Нула вектор - вектор, всички чиито компоненти са нула.
вектор единица - вектор, на дължина, равна на една:
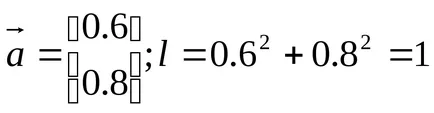
Транспониран вектор - вектор, чиито компоненти са разположени в един ред:
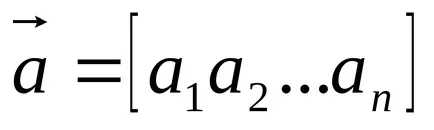
Две вектори на едно и също измерение са равни, когато те са на съответните компоненти:
Наборът от номера подредени в правоъгълна решетка, състояща се от N редове и колони м, наречен матрицата и е означен като:
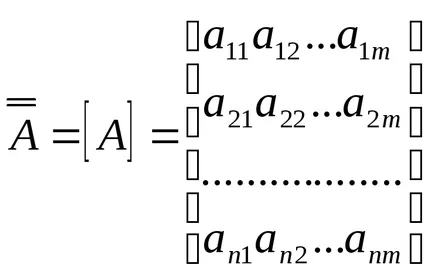
Позицията на елемента

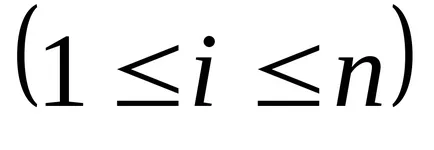
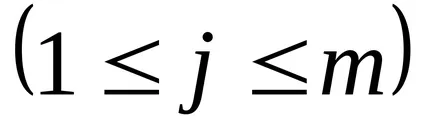
Вектор линия - матрица, състояща се от един ред п = 1
Колона вектор - матрица, състояща се от една колона m = 1
Квадратна матрица - матрица, в която п = m
Горна триъгълна - матрица, чиито
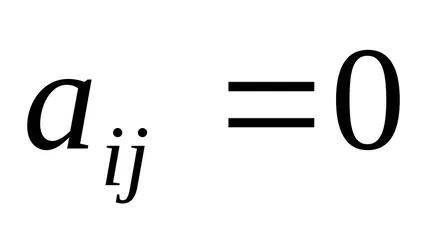
Долна триъгълна - матрица, чиито
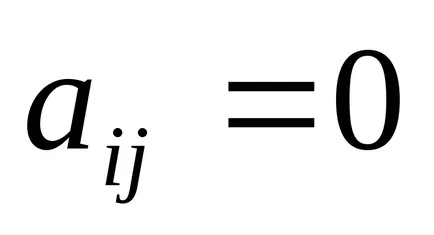
Диагонала - матрица, чиито
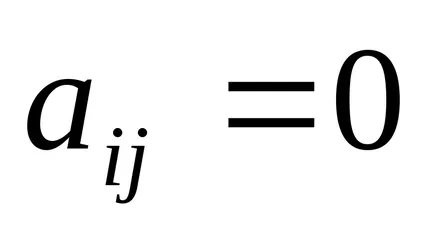
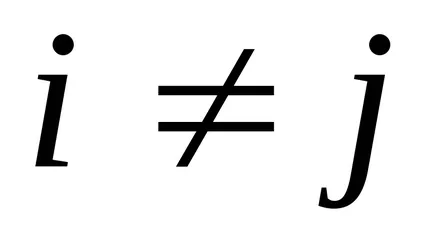
Идентичност - матрица, чиито
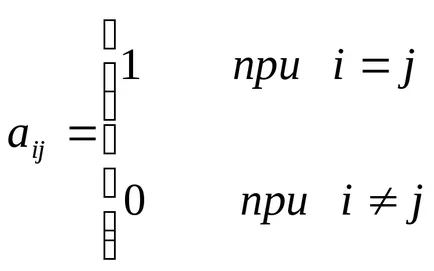
равенство на матрици
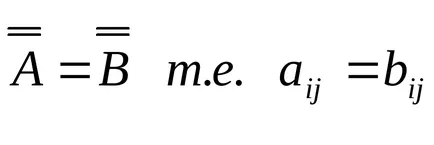
Особености и експлоатация.
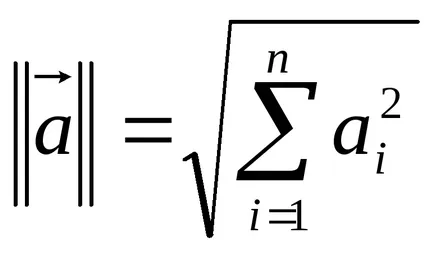
Нормата на матрицата (Euclidean).
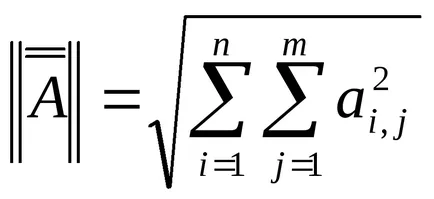
Събиране и изваждане на вектори.
Добави и изважда само вектора с еднакви размери. В резултат на прибавянето (изваждане) е вектор, чиито компоненти са равни на сумата (разлика) на съответните компоненти на две други вектори.
Събиране и изваждане на матрици.
Добави и изважда само матрица със същия размер. В резултат на прибавянето (изваждане) е матрица, чиито елементи са равни на сумата (разлика) на съответните елементи на другите две матрици.
Свойството на добавяне (изваждане) на матриците:
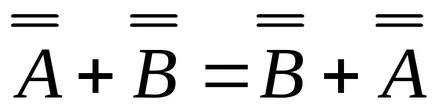
Умножение на вектор с постоянна.
Резултатът от умножението е вектор, чиито компоненти са равни на произведението на съответните компоненти на входния вектор като константа.
Размножаване на матрица от постоянна.
Резултатът от умножението е матрица, чиито елементи са равни на произведението на съответните елементи на оригиналната матрица чрез константа.
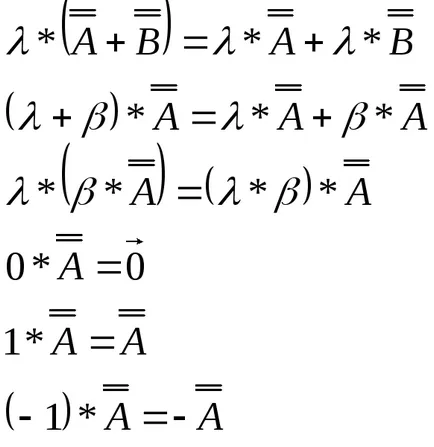
Транспонира матрица - замяна на редовете на колоните, т.е.
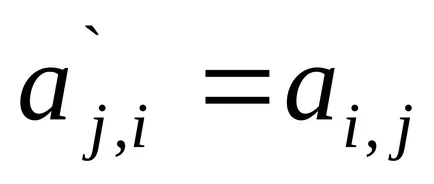
Брой колони на матрицата трябва да бъде равен на броя на редовете на матрицата В.