Уравнение на Бернули
ДЪРЖАВНА МЕДИЦИНСКИ УНИВЕРСИТЕТ на семействата
Наръчник по темата:
Реологичните свойства на биологични течности.
Методи за изследване на кръвообращението.
Основни въпроси, свързани с темата:
- Уравнение на Бернули. Статично и динамично налягане.
- Реологичните свойства на кръв. Вискозитет.
- формула на Нютон.
- брой Рейнолдс.
- Нютонов и Не-Нютонов флуид
- Ламинарен поток.
- Турбулентен поток.
- Определяне на вискозитета на кръвта с помощта на медицински вискозиметър.
- Поазьой право.
- Определяне на скоростта на кръвния поток.
- На съпротивлението на тъканта на тялото. Физическа база на реография. rheoencephalography
- Физични основи ballistocardiography.
Уравнение на Бернули. Статично и динамично налягане.
Идеалът се казва несвиваем и няма вътрешно триене или вискозитет; стационарни или стационарно призова, в който скоростта на флуида частиците във всяка точка на потока не се променя с времето. Характеризира постоянен поток рационализира - въображаемите линии съвпадат с траекториите на частици. Част от течен поток, ограничен от всички страни от настоящите линии, образуващи тръба ток или струя. Изолират ток на тръбата е толкова тесен, че скоростта V на частицата в нейния всяко сечение S, перпендикулярна на оста на тръбата, може да се предположи, еднакви по цялата част. След това обемът на течността, протичаща през всяко напречно сечение на тръба за единица време остава постоянна, тъй като движението на частици в течността се появява само по протежение на оста на тръбата. Тази връзка се нарича с приемственост състояние струя. От това следва, че за реално течност при постоянен поток през тръбата на променлив брой напречно сечение Qzhidkosti, Прото repentieth за единица време през всяко сечение на тръбата, то остава в стойка (Q = конст) и средна скорост на потока в различни напречни сечения, niyah тръба обратно пропорционална области на тези секции: пр ...
Изберете в поток от идеалното епруветка на флуиден поток, а в нея - достатъчно малък обем на течната маса. който, когато Techa-SRI флуид премества от положение А до позиция Б.
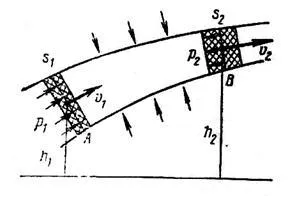
Течности по-даване leniem има вътрешни потенциали, потенциалната енергия (енергия НАЛЯГАНЕ-ционни), чрез които може да не работят. Wp Etaenergiya измерва продукт налягане на обем течност V :. В този случай, течност маса обем се дължи на разликата в налягането сили cheniyah SE-Si и S2. Работата, извършена от където Аг е равна на разликата в налягането енергия потенциално пиксела. Тази работа се изразходва за работа, за да се преодолее действието на тежестта минути сила и кинетичната енергия на изменението на масата
Пренареждане на условията на уравнението, получаваме
Позиции А и Б са избрани на случаен принцип, може да се твърди, че на всяко място по протежение на тръбата текущата състояние продължава
Разделяне това уравнение с. получаваме
където - плътност на течността.
Това е уравнението на Бернули. Всички членове на уравнението, тъй като лесно се вижда, са насочени към интересите на налягане и се наричат статистика: хидростатично - динамичен. Тогава Уравнение на Бернули може да се формулира по следния начин:
при неподвижен поток от идеалното течност общо налягане, равно на сумата от статично, динамично и хидростатичното налягане остава постоянно във всяко напречно сечение на потока.
а-размразява постоянен ток хоризонтална тръба и хидростатичното налягане може да се дължи на дясната страна на уравнение, което по този начин под формата
статично налягане потенциална енергия причинява zhidkos минути (енергия налягане), динамичното налягане - кинетична.
От това уравнение, може да се заключи, наречен Бернули правило:
статично налягане невискозен течност по време на протичане на Hori-Тал увеличава тръба, където се намалява неговата скорост и оборота.