точка фероелектрични Кюри

Ferroelectrics това диелектрици, които имат няколко специфични свойства, които се реализират дължи на факта, че те имат структурата на домейна в определен температурен диапазон може да бъде спонтанно поляризирана, посоката на поляризация могат да бъдат променяни от електрическо поле.

В някои твърди и течни вещества, при определени външни въздействия фазови превръщания възникнат без изменение на състояния на агрегация. Например, пиезоелектричното тяло може да бъде превърнат paraelectric.

Какво е точката на Кюри

Ако фероелектричен повишаване на температурата до определена температура ($ T_k $), който е различен за всяко вещество, диелектричните свойства на фероелектричен изчезва и става обикновен изолатор. Тази точка на фазовия преход от фероелектричен състояние до състояние, наречено точка полярен диелектрик Кюри и съответната температура ($ T_k $) - температура на Кюри. Има ferroelectrics, в която две от точката на Кюри, горната и долната част. Такива материали запазват фероелектрични свойства в температурен диапазон, който предварително определени горни и долни граници. Такива ferroelectrics относително не са много. Повечето ferroelectrics само горната точка на Кюри.

Графика на спонтанното поляризация на пиезоелектричното тяло ($ P_S $) на температура близо до точката на Кюри е показано на Фиг.1.

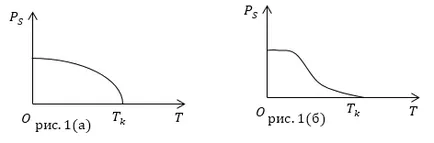
В околностите на прехода фаза (при точката на Кюри) фероелектричен материал структура е ковък на външни влияния. Дори малки промени в напрегнатост на полето близо до прехода от фаза причинява значителни промени в електрическите свойства на диелектрика.

Близо точката на Кюри в ferroelectrics, които са в полярната фаза, стойностите на диелектрична достигат много високи стойности (до $ 4 ^ \ ^ 5) $. Например, бариев титанат $ (BaTiO_3) температура на Кюри $ точка е около 120 $ ^ $ ° С, и диелектрична константа достига максимума на $ $ 6000-7000. Трябва да се отбележи, че има ferroelectrics и не много голям диелектрична константа, например, някои водоразтворими ferroelectrics имат пропускливост $ \ varepsilon = 5-6 $.

Освен това, максималната диелектрична константа при точката на Кюри се постига (Фигура 2).

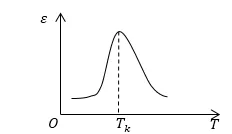
Законът за промяна на диелектрик податливостта

Законът за промяна на диелектрик податливостта на фероелектричният фаза в неполярни около точката на Кюри може да се запише като:

където $ A $ - константа. $ T_0 $ - температура на Кюри - Weiss температура, близка до точката на Кюри ($ T_k $). Много често във формулата (1) вместо да се използва $ T_0 $ $ T_k $. В този случай, ако има два на точката фероелектричният Кюри, втората точка в близост до закона на Кюри-Вайс се изписва така:

В случай на анизотропни диелектрици скаларна $ \ $ varkappa във формули (1) и (2) се заменят със тензорен $ _. $ Температурна зависимост не се променя.

На практика фероелектричният закона Кюри-Вайс може да се запише, за да открие диелектрична константа във формата:

където $ С = \ Frac $ - Кюри-Weiss константа, T_k $ $ - температура на Кюри, в който настъпва преход фаза, и $ \ алфа $ промени знак. Ако C $ \ сим ^ 3 $, фазовият преход настъпва с подреждането на някои от структурните елементи, йони, протони или групи от атоми. Такава преход понякога по-долу: - да разстройство. Ако C $ \ сим ^ 5 $, преходът на изместване спрямо положението на равновесие. Постоянно Кюри - Weiss често се определя от графика на = \ Frac \ лявата (Т \ дясно) $ $ \ Frac.

Трябва да се каже, че различните преходи фероелектрична фаза могат да имат, както първа и втора класа. Чрез ferroelectrics с преход от първи ред (. Фигура 1 (а)) включват тези, които изпитват поляризация скача при постоянна температура и налягане:

където $ F $ - термодинамичен потенциал, равен на:

Чрез ferroelectrics с втори ред фазов преход (Фигура 2 (а)) включват диелектрици чиито диелектрик чувствителност промени рязко при постоянна температура и налягане (?):

Наличието на точката на Кюри е характерно свойство на фероелектричен материал.

Задача: Към калиев фосфат ($ KH_2PO_4 $), който е фероелектричен поляризация, която е причинена от заместване на водородни йони при температури не в близост до точката на Кюри, опитът дава:

Определяне на стойностите на някои променливи са представени от гледна точка на (1.1)? Виж съотношението на вътрешния поле $ \ бета, $ като се използва формулата (1.2):

Като основа за решаването на проблема ще се формула, която определя отношението на диелектрична константа на фероелектричният с температура:

След това, като се сравняват изразите (1.3) и (1.1) получаваме:

В този случай, коефициентът на $ \ бета $ е лесно да се изчисли, като се използва (1.2). получаваме:

Отговор: $ \ бета = 0,567 $.

Задача: дадени две графики на $ \ varepsilon $ (Т) и $ \ Frac \ лявата (Т \ дясно) $ Фигура 3 (а, Ь). Определи до каква фаза на фероелектричният включва графици I и II.

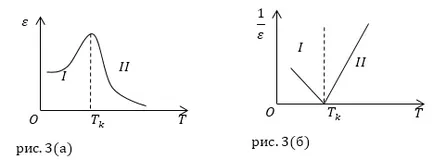
Разглеждане на графиката на фиг. 3 (а). Сегмент на крива белязан позиция I, съответства на пиезоелектричното тяло диелектрик фаза, точка на Кюри ($ T_k $) поляризация достигне максимум сегмент съответства с фигура II paroelektricheskoy диелектрик фаза. Диелектрична константа рязко намалява с увеличаване на температурата, се прекъсва домейн структура на веществото.

Разглеждане на графиката на фиг. 3 (Ь). В съответствие с правото на Кюри-Вайс:

сегмент Аз, се отнася до фазата на - фероелектричен. Обратното на диелектрична константа, намалява линейно с увеличаване на температурата, до $ T> T_k $, когато $ T = T_k $ $ \ Frac = 0 $. Следваща сегмент II - paraelectric при температура по-висока от точката на Кюри.