Тюринг машина
Един от първите формалната дефиниция на алгоритъма е да се определи английски математик A.M.Tyuringa. През 1936 г. той описва схемата на абстрактна машина, състояща се от един безкраен колан и машината, и предполага, наричайки алгоритъм, който е в състояние да направи тази машина. С това определение, нещо, което не може да се направи от една машина на Тюринг не е един алгоритъм. Компютри също са проектирани да изпълняват алгоритмите, но това е истинско устройство, докато Тюринг машината е абстракция. Ние се абстрахира от крайниците на паметта.
А Тюринг машина се състои от една безкрайна в двете страни на лентата разделени на клетки и машина. Всяка клетка може да бъде един от героите от азбуката, които са представени в данните. Ако клетката е празна, тогава ние казваме, че има празно символ. Азбуки могат да бъдат различни, но за определена машина Тюринг избира всяка една азбука. Машината може да се движи по лентата и се редуват "наблюдават" на съдържанието на клетките. Входно дума се поставя върху лентата от една буква в клетките подредени в ред и се краен брой клетки. Най-вляво и вдясно от входната дума за лентата са само празни клетки. Машина е в състояние на предварително определено множество от точки, и една клетка.
Тюринг машини работят задача може да бъде описан като програма - на маса. Във всяка клетка на програмата е необходимо да се уточни какво операции трябва да се извършват автоматично, ако е в определено състояние, той "вижда" това писмо. В общи линии, машината е в състояние да

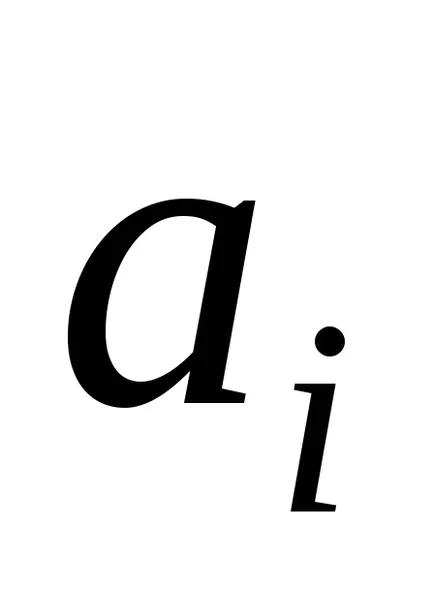
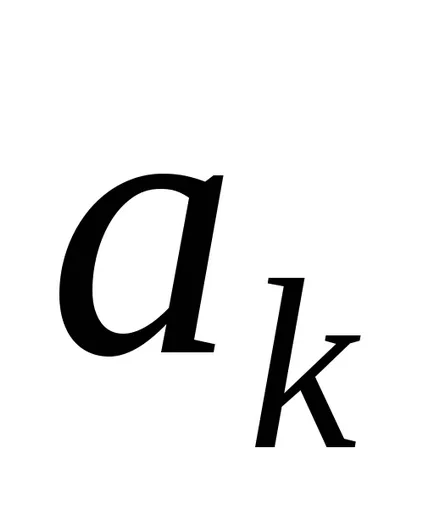


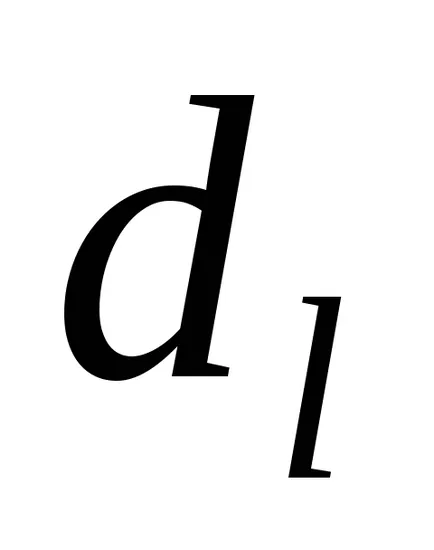
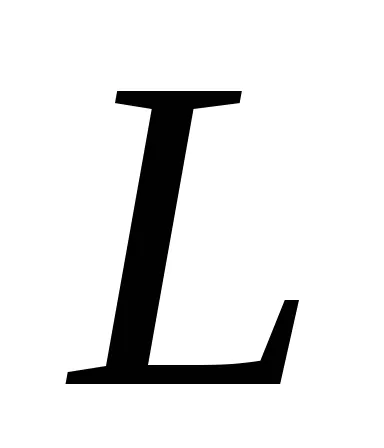
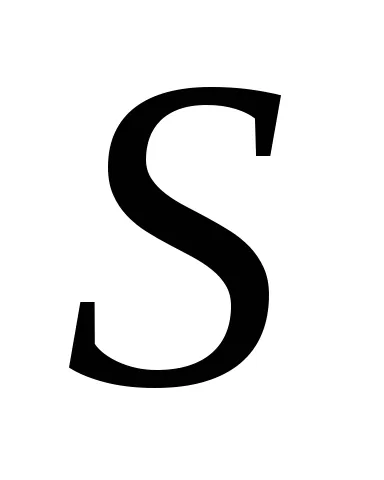

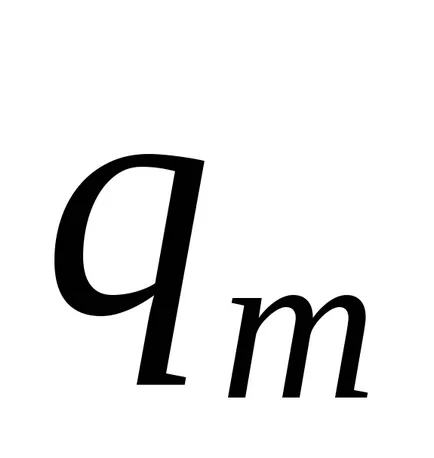
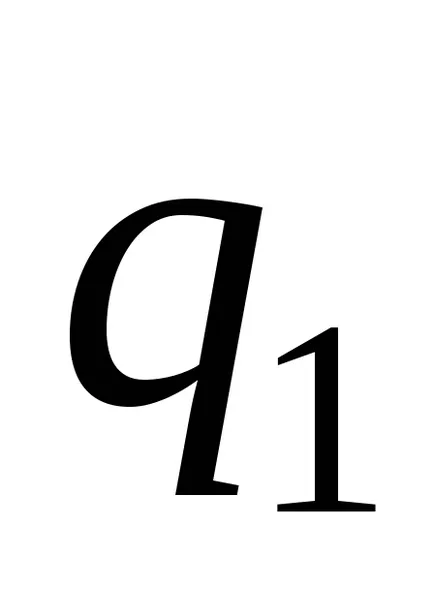
Тюринг машина Configuration е набор от вътрешното състояние състояние на лентата, позицията на лента машината. конфигурация Тюринг машина ще бъде в писмена форма
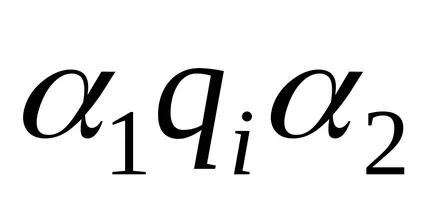
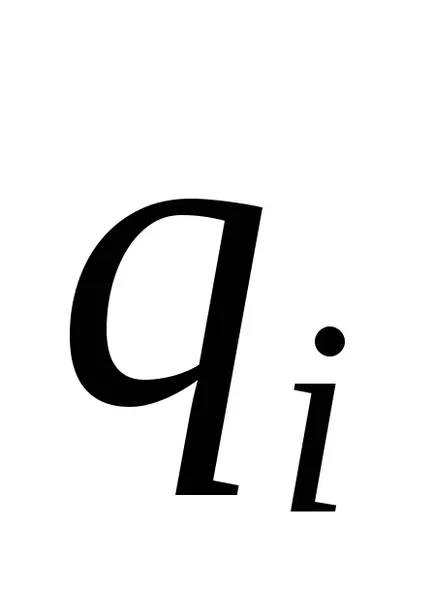

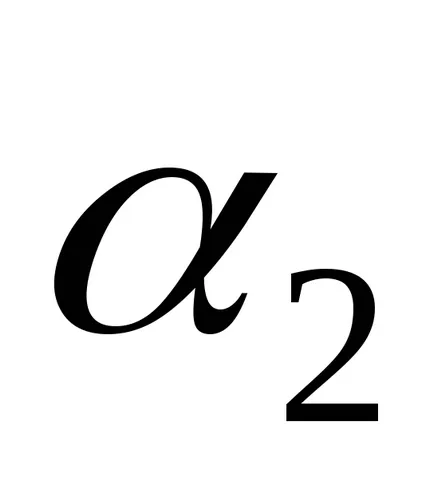
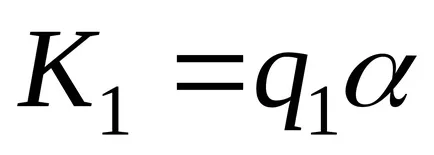
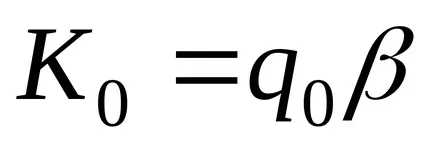
Тюринг машина изчислява частична функция правилно


ако
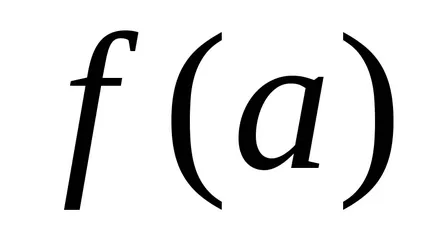
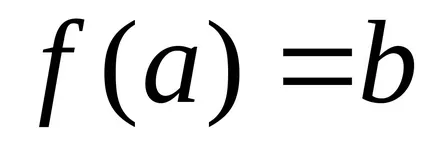
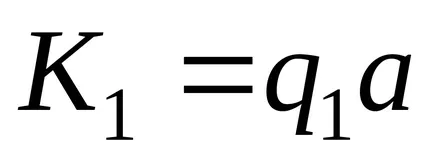
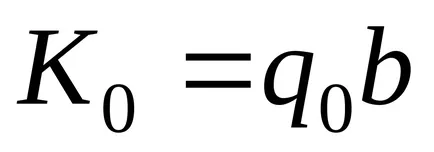
ако
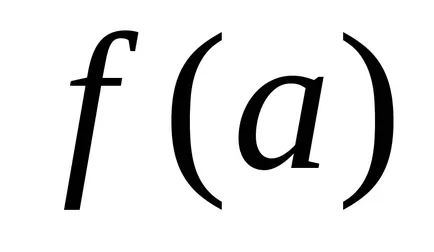
тук

функция
Пример Тюринг машина, която носи първоначалната конфигурация
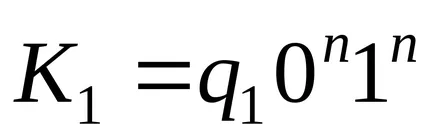
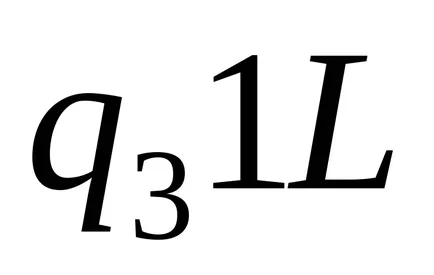
Описвайки различните алгоритми за машини и доказване на осъществимостта на различни композиции алгоритми, Тюринг показа убедително разнообразие от възможности, предлагани от тяхното проектиране, което му позволява да говори със следната теза:
Тюринг теза. Всеки алгоритъм може да се прилага, съответстваща на машина.
Тази теза е официална дефиниция на алгоритъма. Тя ви позволява да се установи наличието или отсъствието на алгоритми, които описват съответната Тюринг машината или да доказва невъзможността да изградят такива. не може да се докаже, Тюринг теза, тъй като формулировката не дефинира понятието "алгоритъм", това е, от лявата страна на идентичността. Тя може да бъде оправдано само чрез представяне на различни добре познати алгоритми под формата на Тюринг машини. Допълнителната подкрепа на тази теза се крие във факта, че по-късно е предложил няколко общи дефиниции на понятията алгоритъмът и всеки път успява да докаже, че въпреки че новите алгоритмични схеми и изглежда по-различно, те всъщност са еквивалентни на Тюринг машини: всичко, което е реализуема в един от тези проекти, Това може да бъде направено в другата. Тези твърдения се оказаха стриктно, тъй като те вече говорим за самоличността на официални схеми.
Марков нормално алгоритъм
През 1954 г. Съветският математик AA Марков предложи различен алгоритмична схема еквивалентно на машина на Тюринг, в който данните се преобразуват на базата на други принципи. В алгоритмична схема Марков няма понятие от лентата, и изисква директен достъп до различните части на преобразуваните думи. Марков нарича алгоритмичен схема на нормалния алгоритъм. Понятието нормална алгоритъм има много предимства, така и основно методичен характер, се оказа ползотворна и удобно. За да издържат на изпитанието на времето и доказа своята жизнеспособност, тя - заедно с концепциите за рекурсивни функции и Тюринг машини - твърдо установени в научната използването на съвременната теория на алгоритмите.
Нормално алгоритъм Марков е подреден набор от пермутации (продукт) на формата
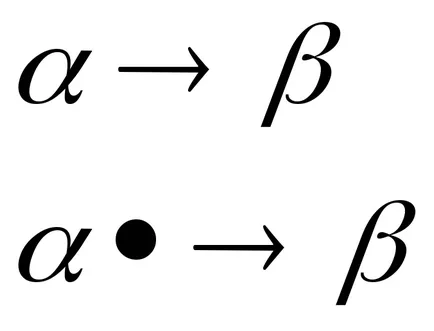
заместване формула се използва за замяна на subwords в трансформиращия дума. И subwords заменяем заместител във формулата са разделени от една от стрелките или → • →. продукти тип

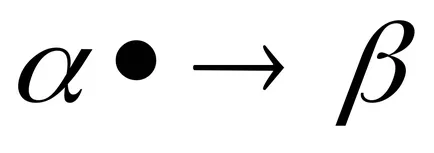
Като пример алгоритъм за изчисляване на функцията в азбуката
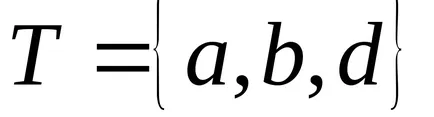

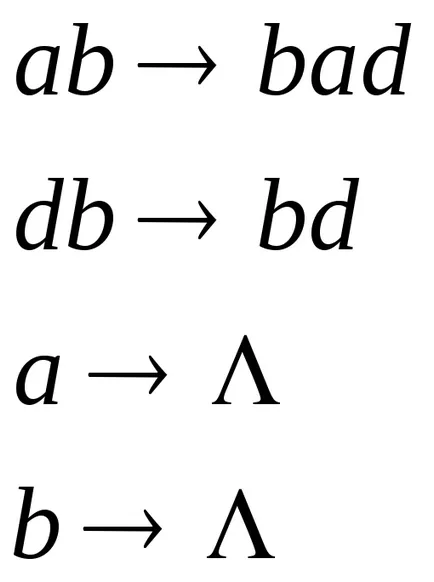
Извършване Марков алгоритъм е разделен на етапи. Всяка стъпка включва намирането на първия ред формула заместване, приложим за трансформиране на думата, и изпълнение, съответстващо на тази формула се заменя. Ако се опитате да се прилага формулата за смяна е, че има няколко повторения на своите заменяеми части, винаги замества първото (най-вляво) поява. Процесът на алгоритъма завършва в два случая:
- или всички формули са неприложими,
- или крайната формула, в която в лявата и дясната стрелка → subword акция е била приложена в последната стъпка.
Във всеки от тези случаи се смята, че нормалната алгоритъм е приложим за дадена суровина дума.
Ако по време на изпълнението на безкраен брой пъти на алгоритъма са прости замествания на формулата, използвана, алгоритъмът не е приложимо към даден вход думата.
Нормално алгоритъм се нарича нормален алгоритъм над азбуката
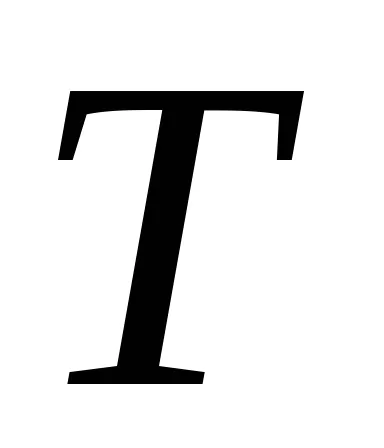
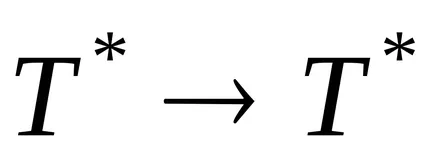

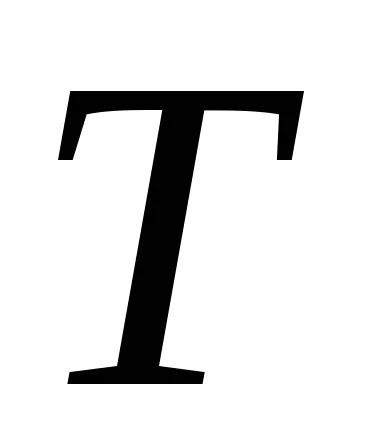
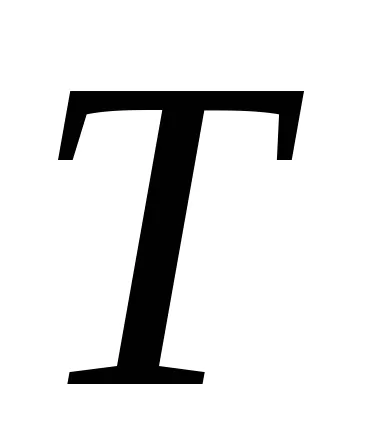
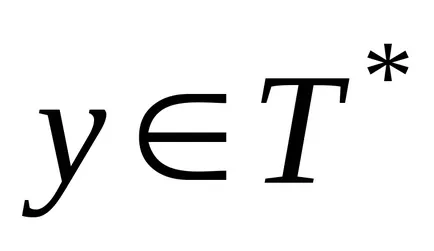
нормално алгоритъм

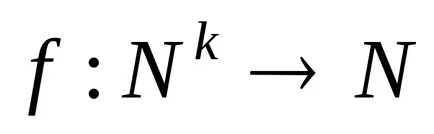

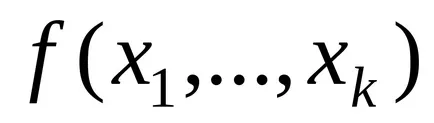
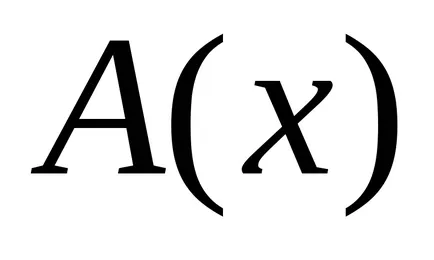
Алгоритмичната Марков Тюринг схема и са равностойни, в смисъл, че всички алгоритми, описани в един от тях може да бъде описан в друга. Тези схеми не могат да бъдат реализирани физически, защото те са математическа абстракция, която позволява неограничени по-голяма дължина думи, настъпили в процеса на трансформация.