теория на игрите
Теорията на игрите. Играта на решение матрица, например.
Играта зададете матрица плащане. За да се определят оптималните стратегии разчитат, първата стратегия дефинира геометрично, а втората стратегия - използване на метода на симплекс.
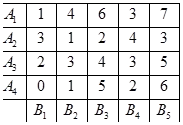
решение:
Разберете, ако има седло точка.
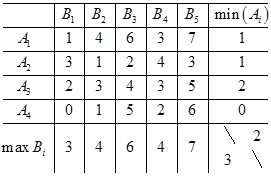
Най-ниската стойност на играта
Най-високата цена на играта
защото по-ниската цена не е равна на най-високата цена, тогава няма седло точка, т.е. решение матрица игра трябва да се търси в смесени стратегии.
Ние разглеждаме матрицата от гледна точка на господстващо положение.
Стратегия доминира стратегия, тъй като всички елементи на петата колона по-големи от съответните елементи на втората колона. Премахване на петата колона.
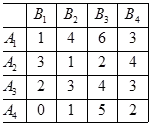
Стратегия доминира стратегия.
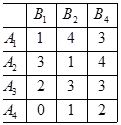
Стратегия доминира стратегия.
Стратегията е строго контролирани стратегия.
Получената матрица на победи, където играчите А и Б не са доминираща стратегия.
Първо, ние намерите играч Б. Имайте предвид, че и решаване на следния проблем на линейното програмиране оптимална стратегия:
Минимизиране на функциите при спазване на ограниченията:
защото само две променливи, а след това задачата на линейното програмиране най-лесният начин за решаване на графично. Ние се изгради набор от изпълними решения, т.е. площ е описано от тези неравенства и ограничена от линиите:
Според х-ос ще се забави. и вертикалната ос. ОБЛАСТ допустимата стойност се сенчести жълто.
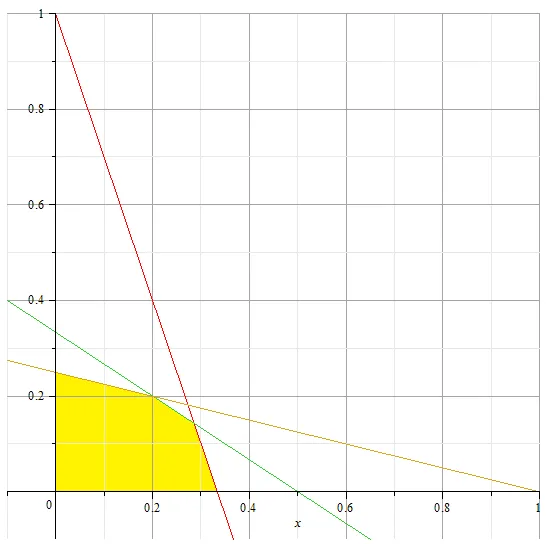
Изграждане на линия ниво. които имат формата. където С - е произволна константа. Ние разбираме, че с цел повишаване на C линия трябва да заемат най-много "високо" положение, но като с областта на изпълними решения, най-малко една точка.
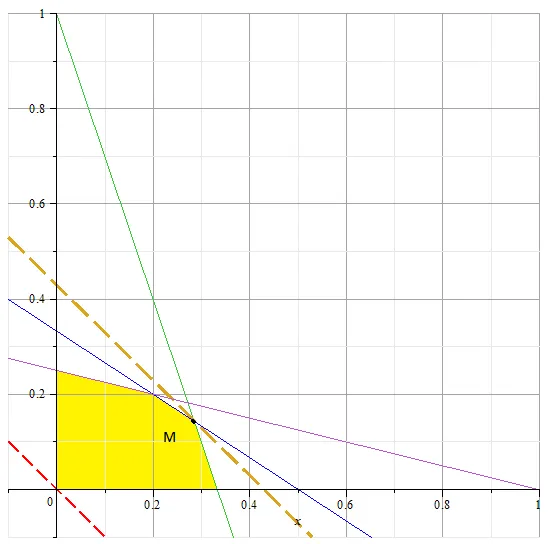
Подобна позиция на линията - минаваща през точка М. Нека намерим координатите му като пресечната точка на двете линии.
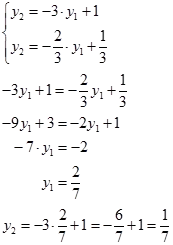
Получихме. след това
и