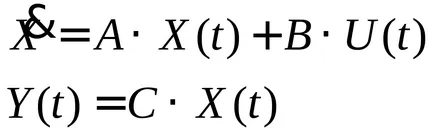Тау определяне sharyakovoy
Редът на най производно определя реда на системата (връзка) като цяло.
Ако п = 1 - система от първи ред; п = 2 - втори ред система.
Функцията за прехвърляне на системата от входа към този изход - съотношението на продукцията изображение променлива на Лаплас на изображението на променлива входни условия на Лаплас и нула точки на входовете равни на нула.
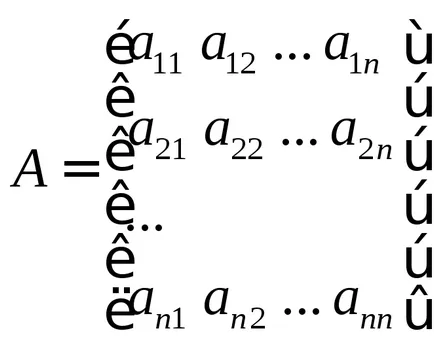
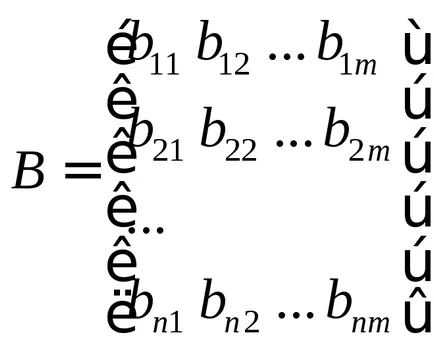
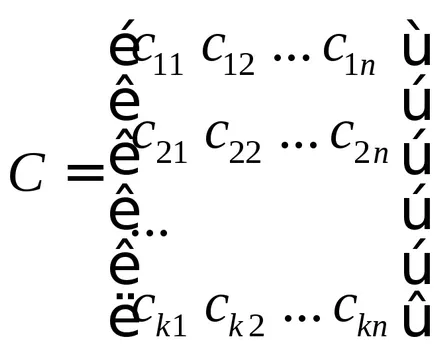
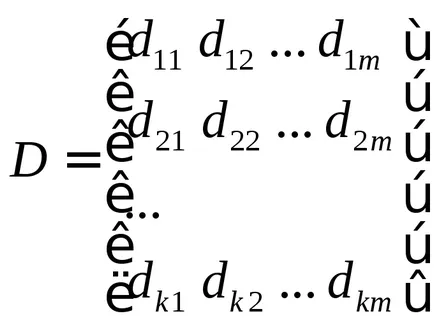
В знаменател на предавателната функция - е характеристика полином на системата. Характерните полином на системата - това е уравнение, което описва свободното движение на системата. Свободно движение на системата - движение в отсъствието на външни влияния.
Преходна функция - това е реакция на системата за единица стъпка функция на формата:
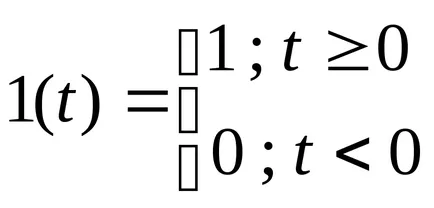
Функцията тегло - отговор система за импулсна функция Дирак на формата:
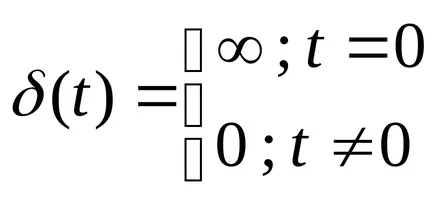
Разследването на свойствата на функцията за делта:
трансфер Честота функция от даден вход на дадена продукция или комплекс коефициента на предавката е съотношението на изображенията на Фурие от изходната променлива да Фурие входно изображение променлива с нулеви начални условия и други материали, равни на нула.
функция на честотата трансфер е комплексно число, чиято модул е съотношението на продукцията амплитуда на амплитудата на входния сигнал. и аргумента представлява фаза смяна между изходните и входните сигнали.
амплитуда честота характеристика на фаза (APFC) - е предавателната функция честота вектор полярен парцел при честота w промяна при -


Corner честота - тази честота е обратно пропорционална на времето постоянно връзката
Стабилност - способността на системата да се върне в някаква степен на точност в първоначалното си състояние след отстраняване на външни влияния, това са излюпени от това състояние.
Определяне на стабилността Lyapunov:
невъзмутим система равновесно положение XE се нарича Ляпунов стабилен, ако за всяко положително произволно малък


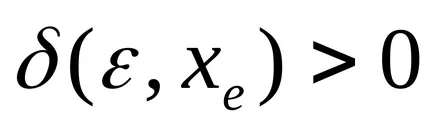

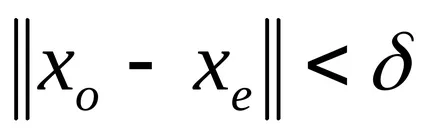

Позиция система ravnovesiyaxenevozmuschennoy нарича асимпотично стабилна. ако тя е стабилна по време на 1 Ляпунов и 2 по какъвто и да е инициирано от нарушен движение

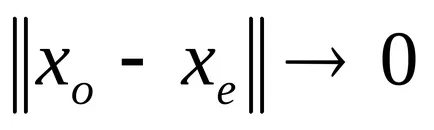
Определяне асимтотична стабилност по-строго, отколкото стабилност Ляпунов.
За това, че системата е стабилна, ако и само ако всички корените на полином характеристика имат отрицателни реални части. Присъствието на поне един корен с положителна реална част ще доведе до нестабилност на цялата система.
Необходимо, но не достатъчно условие за стабилността на линейна система за автоматично управление (ACS) е позитивност на всички коефициенти на характерната полином (JP). Ако поне един негативен фактор - системата е нестабилна.
За SAU линеен асимптотично стабилен, ако и само ако всички фактори на Hurwitz са положителни, ако ао> 0 или отрицателни, ако ао <0.
За да може системата да бъде стабилна, е необходимо и достатъчно. локус Векторът Михайлова D (JW) w, когато се променя от 0 до +

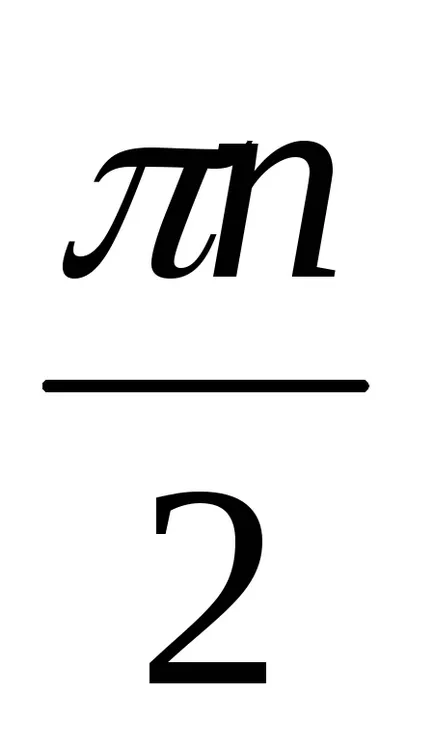
За стабилността на системата е необходимо и достатъчно. на реални и въображаеми корените на функции Михайлов редуват, първата нула корен е коренът на функцията за въображаеми Михайлова.
Характеристики на критерия на Найкуист:
Този тест дава индикация за стабилността на затворената система на честотните характеристики на системата за отворен цикъл.
Редът на HP затворени и отворени системи се равнява на п.
Ако системата за отворен цикъл е стабилна, тогава е необходима и достатъчна стабилност на затворената система. до промяна на тегло -


Ако системата за отворен цикъл е на границата на стабилност, е необходимо и достатъчно за стабилността на системата за отворен цикъл. APFC на отворен контур, допълнена с честота w = 0 безкрайно голям радиус кръг в посока на часовниковата стрелка, не се покрива от точката на реално ос (1; й 0)
Ако системата за отворен цикъл е нестабилна, тогава е необходима и достатъчна стабилност на затворената система. разликата между броя на положителните преходи извършва APFC отворен цикъл, когато честотата w 0 до +


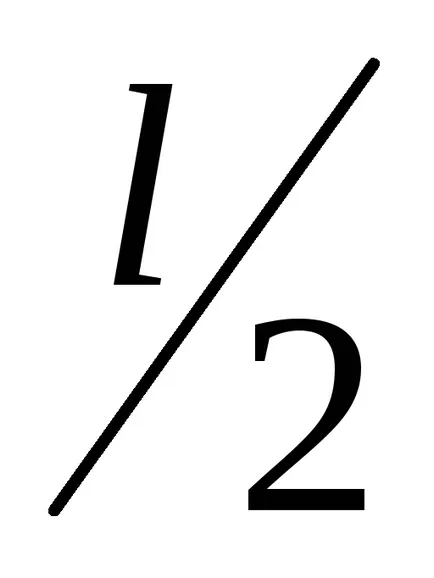
Ако няма sistemaneustoychiva, за стабилността на затворената система, е необходимо и достатъчно. разликата между броя на положителните преходи LPC отворен цикъл през нивата ±

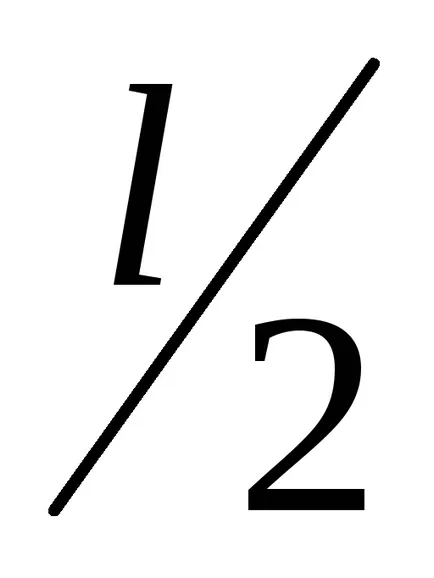
Astatism система с нулев порядък или статична система, такава система се нарича, принудително равновесно състояние грешка, която, когато се прилага към входа постоянен вид сигнал U (т) -U0 = конст е постоянна и пропорционално на входното ниво.
Система с astatism първи ред или астатична система е посочена такава система, принудително равновесно състояние грешка, която, когато се прилага към входа линейно увеличаване на сигнала U (т) = U0 + Vt (U0 = конст, V = конст) при постоянна скорост, постоянна и пропорционално входяща скорост.
Astatism Редът е първата ненулева коефициент на разширяване на грешката.
Astatism възходящ ред в системата, ние се увеличи точността на системата. Но в същото време намалява граница на стабилност във фаза, като поради интегратор Получената LPC отворен цикъл спуска П / 2.
astatism за цел може да се повиши чрез въвеждане на интегратор в предавателната функция на системата за отворен цикъл.
Определяне на astatism на поръчката
1. Блоковата схема
Процедура astatism от входния система е равен на броя на чисти интегратори във веригата за обратна връзка между точката на прилагане на външен сигнал и сигнал за грешка. Интегратори в прекия път между входния сигнал и ако грешката не оказва влияние astatism на поръчката.
Косвени методи за определяне на показателите за качество.
Всяка корен на характеристика полином има своя компонент в процеса на преход. Преходно се определя главно изкорени най-близо до въображаема ос, като съответния компонент отслабва бавно.
1) Степента на съпротивление е равна на реалната част на корена най-близо до въображаемата ос
2) степента на колебание се определя и от горната част, близо до въображаемата ос.
Ако близо до въображаемата ос е истинският корен, трептенията е нула.
2. Интеграл методи.
1) Най-простият неразделна оценката характеризира грешки на затихване. Този тип оценки, подходящ за монотонни преходни процеси.
2) квадратно неразделна оценка.
Недостатък - ако тази оценка да се използва като целевата функция в оптимизацията, можете да получите в силно люлеене в като най-доброто от процеса на преход.
Минимизиране на I2 води до значително първоначалните промени грешки скорост и бързи промени в знак, а оттам и значително превишение и изкълчване.
3) Подобряване на интегрална оценка.
Чрез избиране на параметър Т може да осигури необходимата промяна на наклона на грешката, и по този начин се постигне желаната скорост на намаляване на грешка и качествено преходен процес.
Начини за включване на коригиращи устройства:
1. В съответствие корекция;
2. паралелна корекция;
3. Директно паралелна корекция.
Структурата на подчинен регламента - последователен начин.
1. пропорционален контролер;
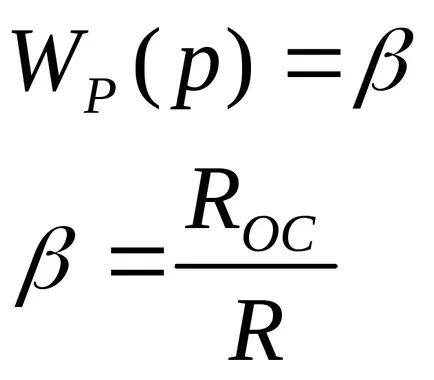
2. интегриран регулатор;
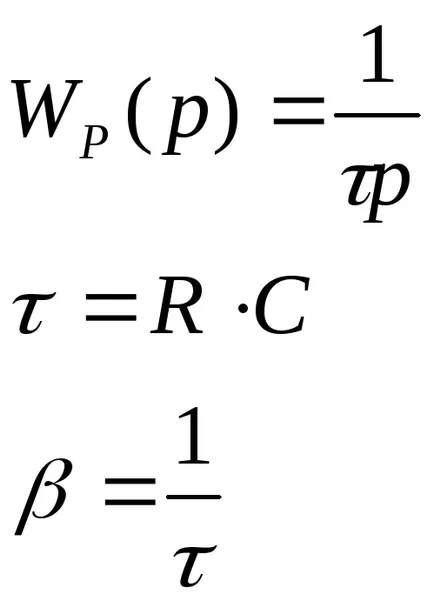
3. пропорционално-интегрален регулатор;
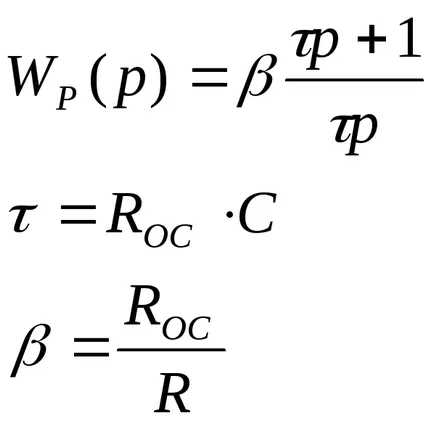
4. пропорционално-интегрален производно контролер
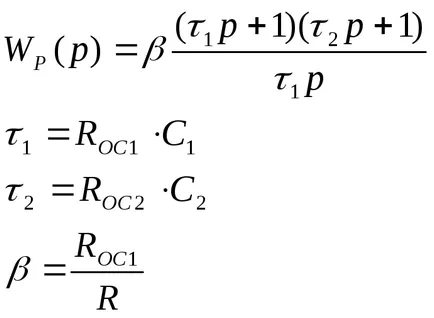
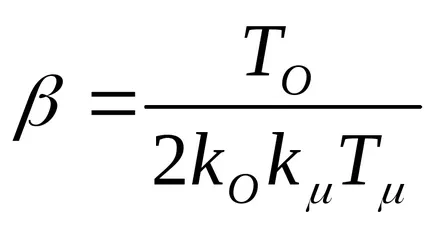
Когато настроена на оптимална модул - добро преходно отговор на контролен сигнал, малка превишаване, висока скорост, но има недостатък - лошо процес преход в нарушаваща влияние.
Когато настроена оптимално уравновесен с - преходния процес е значително превишаване и ниска скорост, т.е. maloudovletvoritelnym е (лош), но има предимство - добра смущение процес на преход.
входно-изходни нарича матрица Н (п) на матрицата на прехвърляне, което отговаря Y (п) = Н (п) • U (р), където елементите на матрицата Н (п) е предавателната функция на системния запис й ред на i- за да излезете.
yavlyaetsyapolnostyu система за управление. ако може да бъде подадена от всяка първоначалното състояние x0 (T) = х (t0) на всеки краен XK (T) = х (ТК) върху ограничен интервал от време.
yavlyaetsyapolnostyu система за управление. ако рангът на матрицата P е от порядъка на системата. (Rang P = N)
Място Matrix - старши не нулев детерминанта на матрицата.
система
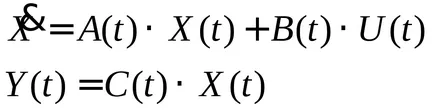
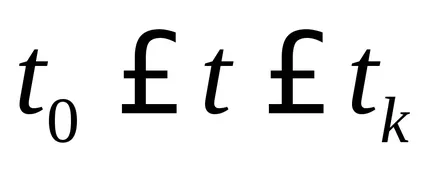
система