Създаване елипсоид на революция
Задача. Елипсоид за два параметъра, посочени в приложението за изчисляване на останалата част от основните параметри и да ги сравните с параметрите на елипсоид WGS 84. Схематично показват отделните елементи в чертежа.
Елипсоид на въртене, нейните елементи и връзки между тях.
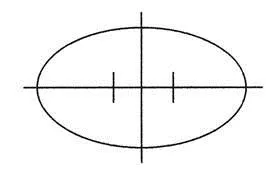
Когато - голям или екваториална ос на елипсоида, - малък или полярен полу-ос (Фигура 1).
Сеченията на елипсоида повърхностни равнини, перпендикулярни на оста на въртене е кръг, наречен паралели. Най паралелно равнина, която минава през елипсоида около центъра, наречен екватора. Екваторът разделя елипсоида на две равни половини: север и на юг.
А равнина, минаваща през малката ос на елипсоида, наречен меридианната равнина, и напречно сечение им повърхност на елипсоида - меридиани.
раздел Меридиан са елипси. разстояние от
център на елипсата на всеки огнища, равен, наречен линеен ексцентричност и съотношение ексцентричност на линеен до голяма или малка ос - ексцентричността на елипсата. Съответно се прави разлика първата и втората елипса ексцентричност меридиан:
Първо ексцентричност - (2)
Вторият ексцентрицитета - (3)
Линейни елементи - Основните и второстепенни полуос - на елипсоида определят размерите и ексцентрицитета - формата си, с други думи, по-голямо или по-малко плоска на полюсите. Колкото по-голяма разлика между големи и малки полуоси, толкова по ексцентрицитета и обратно. В областта е нула.
Елипса форма също определя относителния размер на друга, така наречените полярен сплескването, или просто компресиране на елипсоида, изчислена съгласно формулата: (4)
Както следва от формула (1), елипсоид на въртене е напълно определя от два елемента - малки и големи полуоси. Вместо малка ос често се използва компресия или ексцентричност. Една от двете определени елементи трябва да победи на линията.
Заедно с (2) - (4), съществуват следните връзки между елементите на елипсоид:
Те са резултат директно от формули (2) и (3). Ако сложите:
Чрез прости преобразувания можем да получим:
Polar радиус на кривина (понякога наричан основен) е равен на:
. Основната радиусите на кривина, в някакъв момент, са:
М - в меридианната равнина,
N - в първата вертикална равнина (първата вертикална - равнината, минаваща през нормалата на елипсоид перпендикулярна на меридианната равнина),
- средният радиус на кривината. В екватора, меридиан радиус на кривина (М) е минимална, екватора (N) и средния радиус на кривина (R) определя от израза:
От формулите (4), (7), която е, идващи от.
За наземна елипсоид, с изчисления мерник, може да се приема :.
Стойностите сферична геодезията и определят първи ред, и - втори ред, и така нататък.
Насочване на въртене елипсоид - 4.5 от 5 въз основа на 2 вота