Синус, косинус, допирателна, котангенс произволен ъгъл

За да влезете в определението за задължително, косинус, тангенс и котангенс за произволен ъгъл, ние използваме тригонометрични кръга.

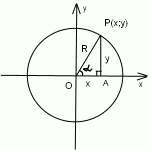
Помислете за един правоъгълен триъгълник AOP. По дефиниция на тригонометрични функции на остър ъгъл, ние имаме:

\ (Sin \ алфа = \ Frac \ защото \ алфа = \ Frac \ ТГ \ алфа = \ Frac \ CTG \ алфа = \ Frac \). Но \ (ОА = х, АР = Y, OP = R \). Следователно, \ (син \ алфа = \ Frac \ защото \ алфа = \ Frac \ ТГ \ алфа = \ Frac \ CTG \ алфа = \ Frac \).

Промяна на радиуса на окръжността не се отразява ценностите на синуса и косинуса. Поради това е удобно да изберете R = 1. Този кръг се нарича единица. По този начин, \ (син \ алфа = Y \ защото \ алфа = х \).

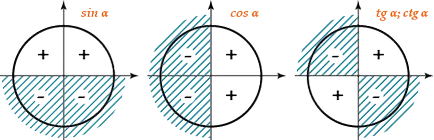
В повечето случаи, единичната окръжност използван при определяне на знака на тригонометрични функции, числови стойности или таблици са изчислени с помощта на калкулатора.

Стойностите на тригонометричните функции, които трябва да знаете наизуст.

Като произволен ъгъл \ (\ а \) и преминава напълно пълен кръг, се върнем към същия ъгъл \ (α \).

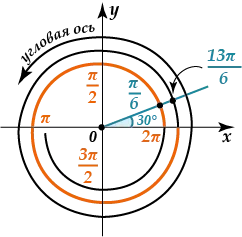
\ (Sin (α + 2πk) = sinα \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ТГ (+) = TG α cosα \ \ \ \ \ \ α πk \\ COS (α + 2πk) = \ \ \ \ \ \ \ \ \ CTG (α + πk) = CTG α \)

Синуса и косинуса са периодични функции с период 2π.

Тангенсът и котангенс са периодични функции с период π.