симетрията на осово и централната
Движение - картографиране на самия самолет, при който се спазват разстоянията между точките. Ако две форми се комбинират (отливка) помежду си чрез движение, тези цифри са еднакви, са равни.
Един от тези движения - аксиална симетрия. Всяка точка в равнината на определен закон е свързан с различен точка на една и съща равнина.
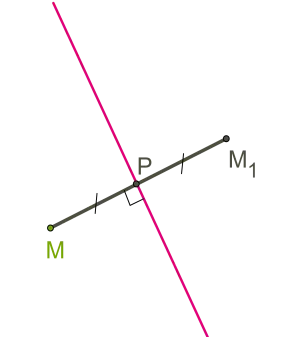
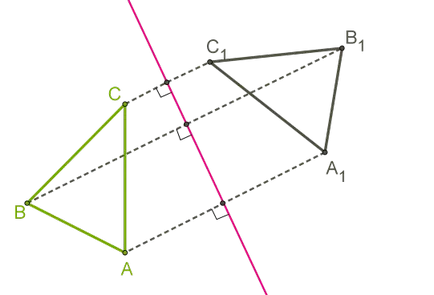
Точки М и М1 са симетрични по отношение на линията, и ако тя преминава през MM1 сегмент център. и ако тя е под прав ъгъл към този сегмент. Всички точки считат за преки и се считат за симетричен за себе си. Фигурата се счита за симетричен по отношение на права линия, като че ли за всяка точка на форма симетричен до точката, че сравнително прав и е на фигурата. Директен и в този случай е оста на симетрия на фигурите (фигура с аксиална симетрия).
Друг специален случай на самолета на дисплея на централна симетрия. Точка M самолет се движи до точка M1 самолет по следния начин:
1. От гледна точка М на права линия, свързваща точката на центъра на симетрия (О точка).
2. На отсечката се забави OM1 = ОМ, и е точката М1.
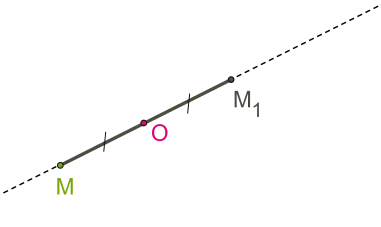
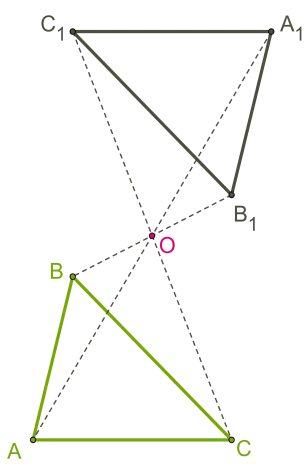
Фигурата е симетрична около точката O ако за всяка точка на симетрична форма е също точката на фигурата. Точка O е център на симетрия. Има данни с централната симетрия е, например, кръг и успоредник. В периферията на центъра на симетрия - е център се намира в центъра на симетрия на успоредник - момент, в който го пресича по диагонал.
Фигура паралелно превод се нарича прехвърлянето на всички точки в пространството на едно разстояние в една посока.
Паралелно транспорта определя вектор, на която се извършва прехвърлянето.
За да направите паралелно предаване, което трябва да знаете посоката и разстоянието, което се задава вектор.
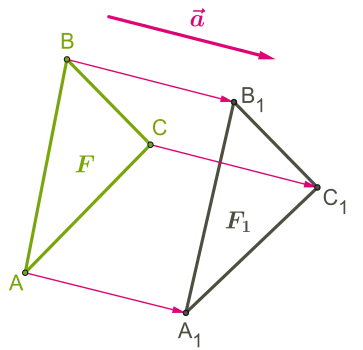
Паралелно трансфер магазини разстояние и посока, т.е. AB = А1 В1.
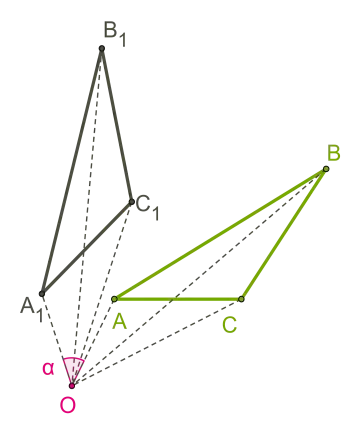
Ако една част се получава от други части на неговото въртене около централната си точка о под същия ъгъл в същата посока, като форма на трансформация се нарича въртене.
За да се проведе, то трябва да се настрои на центъра О, и ъгъл на завъртане алфа.
Обратно на ъгъл положителен въртене обратно - ъгъл отрицателно въртене (както и ъглите на въртене в кръг единица).
Означаваме равнина точка о (център на въртене) и определят ъгъл α (ъгъл на въртене). Триъгълник ABC върти в положителна посока (приблизително а = 45 °). В този случай, на точка O остава на мястото си, която се показва в себе си, както и всички останали точки се завъртат около точка O в същата посока - .. посока на часовниковата стрелка или обратно на часовниковата стрелка.