Резюме брой система - на брега на реферати, есета, доклади, курсови работи и дисертации

Каква е системата на номер?

Той генерира числа в позиционна бройна система?

Защо хората използват десетичната система, както и компютри - двоичния код?

Защо компютрите се използват като осмична и шестнадесетична бройна система?

Преводачески номера от един номер система в друга

Добавяне в различни бройни системи

Изваждане в различни бройни системи

Умножение в различни бройни системи

Разделението в различни бройни системи

Каква е системата на номер?

брой система - набор от методи и правила, за които номера са записани и прочетени.

Има позиционна бройна система и nonpositional.

В nepozitsionnyh брой системи фигури тегло (т. Е. принос за стойността на броя) е независима от нейната позиция в номера на запис. Така че, сред XXXII (тридесет и две) цифри х тегло при всяко положение е само десет в римски цифри система.

В позиционни цифра системи теглото на всяка цифра се променя в зависимост от позицията (позициите) в последователност от числа, които представляват броя. Например, сред първите Групата на седемте 757.7 означава 7 стотици, а вторият - 7 единици, а третият - 7 десети от единица дял.

Същият запис броя на 757.7 е съкращение израз:

Всяко позиционна система номер се характеризира с основа.

В позиционна система на номериране база - броя на различни цифри, използвани за представяне номера в този формат.

За основата на системата може да отнеме всяко физическо брой - две, три, четири и т.н. Следователно, може би безброй позициониращи системи: двоична, троична, четвъртичен и т.н.

Той генерира числа в позиционна бройна система?

Във всяка система радикали номера са подредени съгласно техните стойности: 1 е по-голяма от 0, по-голямо от 1 2 и т.н.

Prodvizheniemtsifry нарича заместител следващото си най-големият.

Насърчаване на броя 1 след това да го замени с 2-цифрен 2 средства за насърчаване промяна това до 3, и т.н. Насърчаване на най-ниската цифра (т.е. номер 9 в десетичната система) означава, че замяната на 0. В двоична система, която използва само две цифри - 0 и 1, 0 средство за насърчаване на замяната на това от 1, както и насърчаване с 1 - 0, за да го замени.

За образуването на редица след всеки даден число, което трябва да се насърчава най-дясната цифра на числото; Ако някоя цифра след края на промоцията е станал нула, тогава ще трябва да се движат цифра вляво от него.

Приложението на това правило, можем да запишем първите десет числа

в двоичен 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;

в трикомпонентна система: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;

на петорен система: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;

осмично 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.

Също така широко използвани знак система с база, която е неразделна мощност от 2, а именно:

Защо хората използват десетичната система, както и компютри - двоичния код?

Хората предпочитат десетичната система, вероятно защото от древни времена се счита, от една страна, и на хората от десетте пръста на ръцете и краката. Не винаги и не навсякъде хората използват десетичната система. В Китай, например, отдавна се радва на петкратното система номер.

Но компютрите използват двоична система, защото тя има няколко предимства в сравнение с други системи.

необходими за нейното реализиране технически устройства с две устойчиви състояния (т.е. тока - без ток магнетизираната - не магнетизираната, и други подобни), вместо, например, десет, - като десетична;

Информацията е предоставена от едва две държави надеждно и имунитета;

primenenieapparata възможно булева алгебра да изпълнява логическа информация трансформация;

двоична аритметика много по-лесно десетични.

Липсата на двоична система - бързото нарастване на броя на битовете, необходими за записване на номера.

Защо компютрите се използват като осмична и шестнадесетична бройна система?

Binary система, удобно за компютри, за човека е неудобно, защото на неговата обемност и необичайни записи.

Превод номера от знак за двукомпонентни и обратно изпълнява машина. Въпреки това, за да използвате компютър, професионално, трябва да се научат да разбират думата машината. За това и предназначени осмични и шестнайсетични системи.

Цифрите в тези системи се чете почти толкова лесно, колкото десетичната изискват съответно три (осмична) и четири (шестнадесетичен) пъти по-малко битове от двоична система (за броя 8 и 16 - съответно третата и четвъртата власт от 2) ,

Преводачески номера от един номер система в друга

Брой на стр различни номера, използвани в системата за позициониране определя име и номер на системата за нарича бройна система база - "Р". Всеки номер N в позиционен номер система с база р може да бъде представена като полином р база:

тук N - брой, ай - коефициенти (брой цифри), р - корен (р> 1). Приети представлява номера като поредица от числа:

Превод номера в десетичната система се извършва чрез теглене мощност серия към основата на системата (виж екв. 1.1), от които броят се превежда. След това изчислява стойността на сумата.

Ако искате да прехвърлите от корен S в R, при условие, че те не са кратни. тогава ще трябва да се опитаме да вземем К. номерация система, така че: S = KN и R = KN.

Превод 175248 "16" SS

Резултат: 175.248 = 7D.516.

Ако K е системата брой не може да вдигне, а след това ще трябва да завършите прехвърлянето използване междинен десетичната система.

За всичко това, примери

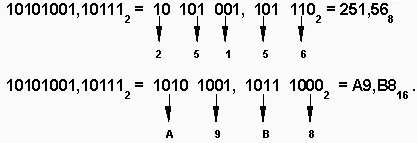
Превод осмична и шестнадесетична числа в двоична система е много проста: това е достатъчно, за да замени всяка цифра от двоичен еквивалент триада (тройните цифри) или преносим компютър (с четири цифри).

За да се превърне броя на двоичен да осмично или шестнадесетичен, е необходимо да се раздели отляво и отдясно на десетичната точка в триада (за осмична) или четворка (шестнадесетично), и всяка такава група, която да замени съответната осмична (шестнадесетичен) цифра. Например:

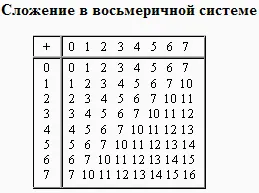
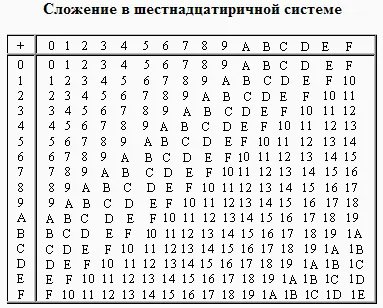
Добавяне в различни бройни системи

таблицата на допълнение е лесно да се направи, като се използват правилата за преброяване.

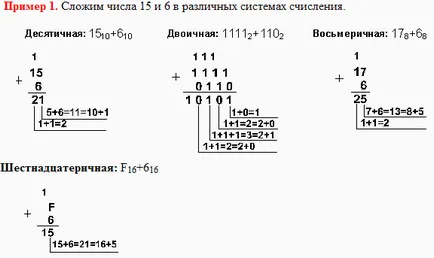
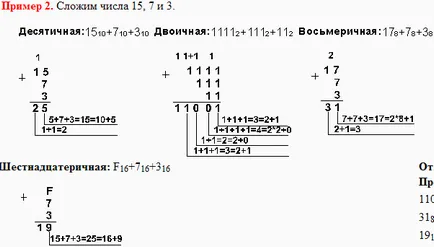
Изваждане в различни бройни системи

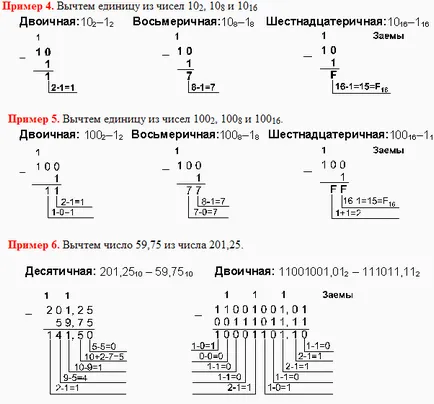
Умножение в различни бройни системи

Извършване умножение на multidigit номера в различни позиционни системи за номериране може да се използва конвенционален алгоритъм за умножение на числа в колоната, но резултатите от умножение и допълнение трябва да бъдат едноцифрени заемат от системата по съответните присъединителни и умножение таблици.

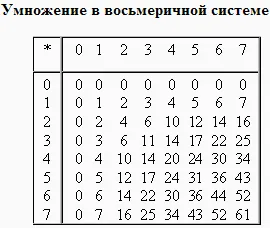
Разделението в различни бройни системи

Разделяне всеки позиционна бройна система е направена от същите правила като разделението на ъгъла в десетичната система. Двоичното разделянето се извършва изключително лесно, тъй като друга фигура на частния може да бъде само нула или един.