Решаването на проблемите на диференциални уравнения и серия, страница 3

Една серия променлив е, следователно, следствие функция Лайбниц. Очевидно е, че трети мандат на поредицата, така п = 2 и до 0001:

.

За да се изчисли, например, трябва да се постави в радиани.

б) За да се изчисли първия подарък, така че да можем напишете:

.

На следващо място, ние прилагаме Тригонометрия поредицата, в която вярват. В нашия случай :.

Ние влагаме в редица, а след това

,

.

От третия елемент, следователно, и с точност от 0,001 :.

4.11. Изчисление на интеграли с помощта на серия

Тъй като срокът за захранване серия от термин може да се интегрира във всеки сегмент се намира в границите на интервала на сближаване, а след това чрез разширяване на подинтегрален в серията енергия е възможно да се намерят на приблизителна стойност на определен интеграл.

Пример 1. Изчислява се доближава до най-близкия 0.001 определен неразделна :.

Решение. В подинтегрален е такава, че неговата примитивна не може да бъде изразена по отношение на елементарни функции. Е приложима за редица, получаваме:

,

,

тъй като третият член получава променлив серия е по-малко от 0,001.

Пример 2. Изчисли приблизително до 0,01 интеграл:

.

Решение. Antiderivative функция също не може да бъде изразена по отношение на елементарни функции:

,

за всякакви х (в този случай, ние използвахме серия Maclaurin за функцията)

За оценка на използването на останалата част от резултата от Лайбниц функция не се осъществи, тъй като не се получава серия променливо. Продължете, както следва:

.

Скобите са получили сумата от безкраен геометрична прогресия, което е 1 :. Ето защо.

Изчисляване на правото на това неравенство за различни п (п = 1, 2, 3, 4), ние виждаме, че за п = 4 :. Ето защо, за да се изчисли на интеграл от до 0.01 е достатъчно да се вземат S4. т.е.

.

4.12. Приблизително разтвор на диференциални уравнения

Понякога именно интегрират диференциално уравнение се провали. В този случай, че е подходящо да се търси решение под формата на поредица власт.

Пример 1 се дава диференциално уравнение. Виж конкретен разтвор отговаря на първоначалното състояние у (1) = 1, под формата на серия Тейлър (като първите 5 членовете).

Решение. Нека решението е

първоначално състояние у (1) = 1, първата срока на тази серия. Заместването х = 1 и у = 1 в уравнение, ние получаваме :.

Разграничаваме оригиналното уравнение:

, , ,

, ,

и т.н. Ние замени намерени в серията стойности, получаваме:

Пример 6 2. Виж първите условията в разтвори мощност серия разширяване на диференциално уравнение, което отговаря на първоначалните условия у (0) = -2.

Решение. Тъй x0 = 0, след това разтворът се иска под формата на серия Maclaurin

.

Предвид това, че Y (0) = -2. Замествайки в това уравнение на първоначалните условия, ние получаваме: Чрез диференциране на оригиналната формула, ние откриваме, последователно:

, , ,

, , .

Заместването намерени в серията стойности, получаваме:

.

4.13. Редове на Фурие

Пример 1 разширена в функция на Фурие е а (х), който има предварително определен период от време и 2p в интервал (-р р] както следва .:

Решение. е (х) функция има точка на прекъсване (фиг. 4.2).

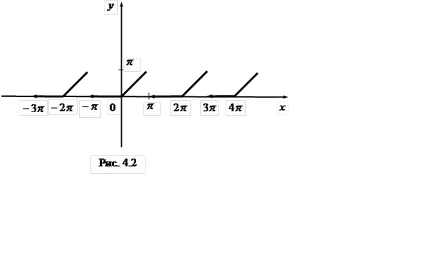
Тъй като е (х) по части монотонно и има за интервал [-p. р] е само една точка на прекъсване на първия вид (), тогава всички точки х на непрекъснатост на F (X) могат да бъдат експандирани в серия Фурие. Ние откриваме редица фактори:

.

,

Н и N. Замествайки тези коефициенти в един ред, получаваме:

за всички, К Z. Броят на точките на размера Намерено:

.

Пример 2 разширена в Фурие серия периодична функция е (х) с период
2л = 4, определена на интервала (-2, 2] от уравнение: F (х) =.

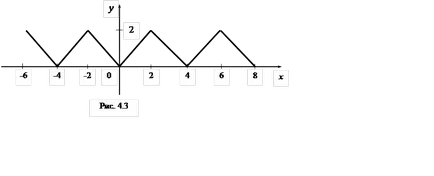
Решение. F функцията (х) се определя и непрекъснато по цялата реалната ос и по части монотонна на сегмент [-2, 2] (фиг. 4.3).

Ние изчисляваме коефициентите на Фурие серия:

,

.

При изчисляване млрд ползване имот от нечетен функция:

,

тъй като подинтегрален е странно. Серията на Фурие за функцията клони към тази функция за всички х. тъй като е (х) е постоянно за всички х. По този начин,

.

1. Обикновени диференциални уравнения. 4

1.1. Проблеми, които водят до обикновени диференциални уравнения. 4

1.1.1. Проблемът на свободно падане на тялото. 4

1.1.2. Проблемът на преходни процеси в електрическата верига. 5

1.1.3. Проблемът на радиоактивното разпадане. 6

1.2. Основни понятия и концепции. 6

1.3. Геометричната смисъла на уравнението. 9

1.4. Основните класове на първите, за диференциални уравнения. 10

1.4.1. Диференциални уравнения с разделящи се променливи. 10

1.4.2. Хомогенни диференциални уравнения. 11

1.4.3. Линейни диференциални уравнения. Уравнение на Бернули. 12

1.4.4. Обикновено диференциално уравнение. 14

1.5. Диференциални уравнения на по-висок ред. 17

1.5.1. Формулите, които позволяват намаляване на поръчката. 17

1.5.2. Линейни диференциални уравнения на наш ред. 21

1.5.3. Линейни хомогенни втори ред диференциални уравнения с постоянни коефициенти. 24

1.5.4. Линейни нехомогенни диференциални уравнения от п-ти ред. 28

1.6. Система от обикновени диференциални уравнения. 33

1.6.1. Методът за отстраняване на неизвестни. 34

1.6.2. Системи линейни диференциални уравнения с постоянни коефициенти. 36

2. Числено серия. 39

2.1. Концепцията на цифров серия. 39

2.2. Достатъчен за сближаването на серия с положителна светлина. 42

2.3. Редуването на реда. Една серия променливо. 48

3. Функционално серия. 52

3.1. Концепцията за функционална серия. 52

3.2. Генератори от серията. 54

3.3. Свойства на мощност серия. 58

3.4. Тейлър серия и Maclaurin. 59

3.5. Използването на мощност серия. 64

3.6. Редове на Фурие. 67

4. Решението на проблема. 74

4.1. На диференциални уравнения на първия ред с разделящи се променливи. 74

4.2. Хомогенна първи ред диференциално уравнение. 74

4.3. Линейно диференциално уравнение от първи ред. 75

4.4. Диференциални уравнения от по-висок порядък, позволяващи намаляване на ред. 77

4.5. Линейни втори ред диференциални уравнения с постоянни коефициенти. 78

4.6. Системи линейни диференциални уравнения с постоянни коефициенти. 78

4.7. Признаци на сближаване на серия с положителна светлина. 78

4.8. Редуването на реда. Лайбниц маркер. 78

4.9. Генератори от серията. Тейлър серия и Maclaurin. 78

4.10. Изчисляването на приблизителната стойност на функцията. 78

4.11. Изчисление на интеграли с помощта на серия. 78

4.12. Приблизително разтвор на диференциални уравнения. 78

4.13. Редове на Фурие. 78

Тест. 91

Правила за изпълнение и тест регистрация. 91

Проблеми за тест. 92

Изпитни въпроси. 96