Развитие на размита алгоритъм за търсене на базата на Hash Публикация в списание "млад учен"
Целта на тази дейност е да се разработи оптимален алгоритъм за търсене размита, речник база данни.
В хода на работата се извършва на алгоритъм за търсене на базата на хашиш. Основният показател, който се използва за сравняване на низове - Левенщайн разстояние. Този алгоритъм трябва да бъде достатъчно ефективна, за да се намали времето за търсене като Левънстийн показателите имат квадратно сложност.
Ключови думи: размита търсене, Левънстийн разстояние, хеширане
Общи проблеми на размита търсене.
Под размита търсене означава търсене по ключови думи, като се вземат предвид възможните случайни грешки в писането на ключовата дума, или, напротив, правописни грешки в целевата заявката.
Ключовият момент за изграждане на компетентен изследвания е изборът на мярка за сходство между думите или, както ги наричат, функцията на разстоянието между думите, които ние наричаме метриката.
Друг важен аспект е правилното индексиране елементи за бърза и надеждна търсене. Използвайте думи сравнителни показатели достатъчно консумират работа, затова е необходимо да се разпределят подмножество на първоначалното речника, които могат да съдържат елементи на заявката за търсене.
Изборът на думи, сравняващи показатели.
Най-често срещаният метриката е показател Лоуенстайн. Левънстийн разстояние - е най-малкият редактиране разстояние така, че един ред отива в друга. Този показател е много популярен и широко използван, така че ние няма да се спирам на него по-подробно.
В случай на сравнение на линии за предпочитане е да се изчисли разстоянието до всяка дума поотделно, а не за целия ред. Освен това е необходимо да се извърши нормализиране да се направи оценка на сходност коефициент думи. В нашия случай, това съотношение ще се изчислява по следната формула:
,
където г (S1 (I), S2 (I)) Левенщайн разстояние, п - брой думи в един ред (обикновено Lang п = 3); S1, S2 се състои от поредица от думи, така че ние се изчисли Левенщайн разстояние за всяка двойка от думи; к - показва сходство на две последователности от думи (две SIF).
речник метод индексиране.
Изчисляване на разстоянието Левенщайн има квадратно сложност, така че е много важно, за да изберете речника в първоначалния комплект, който ще съдържа оригиналната заявка. Подобни методи се основават на вземане на проби, т. Е. Разпределяне характерни елементи на редовете. Най-подходящ метод за малки бази данни (хиляда до 500,000. Речник елементи) е хеш на подписа [1]. Този подход осигурява най-добрата комбинация от търсене на качеството и скоростта на обработка на заявката. Той има предимство пред други методи, като например Soundex (metaphone), N-гр, търсене дърво, тъй като позволява да се правят грешки във всяка част на думата и по този начин търси качество не се разгражда. Това е от съществено значение при превода на български имена на латиница. Освен това, като метод за ускоряване на търсенето на всеки език. Един пример за такава функция може да бъде. Тази функция се препоръчва в [5]. Тази функция е подходяща за четене на речника с дисково пространство, но тъй като в този случай целият речника е заредена в паметта, най-подходящият вариант е по следната формула :, ф (I) - речник елемент, к = дължина (ф (I) ). Ние обобщим всички уникални стойности на низ от символни кодове и да получи определен образ. По този начин, ние ще изгради surjective картиране на елементи на речника в набор от снимки и получи вектор колона, където п - размерът на речника
Описание на използвания алгоритъм, и сравняване на резултатите.
Алгоритъмът за търсене ще се осъществява, както следва:
- речник подредени във възходящ ред стойности з (I) - хеш стойности
- U (1): където у - искане за въвеждане на изображения
- к = koeff (ф (I), а), - изчисляване подобие коефициенти; ако намерите елементи с к = 1.0, търсенето е приключило.
- U (2) =, т = макс (байта (знак)) - максимална стойност на кодовия символ
и така нататък. Разширяване проба подгрупа се ограничава броя на равен на максималния допустим брой на вмъкване грешка или заличаване. Променливата Т на всяка стъпка се увеличава, т.е.. E. Ние първо търси точно съвпадение на изображението (т = 0 * т), наричан по-Т = т * 1 и търси елемент в този набор (няма елементи от предишното), и т.н., за удължаване на максималната брой пъти.
Използването на този метод на индексиране и използване на метричната Левънстийн, можете да постигнете следните резултати. Цифрата показва сравнение на търсене и индексиране на скоростта, без да се използва метода на индексиране, предложен в нашата работа. За точност на резултатите, използвани вход набор от 20 елементи (20 искания за всеки размер на речника) и времето се измерва.
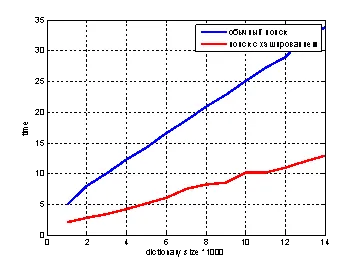
Фиг. 1 Сравнение на разходите от време за конвенционален търсене и търсене на хеширане
Виждаме, че с увеличаването на размера на речника, който печели все по-важно. Освен това в разглеждания пример случай, когато речника не съдържа необходимата искането и допустимата грешка 3. В търсене на реалната ситуация, предложеният алгоритъм ще отнеме много по-малко време.
Сега сравнете алгоритми за търсене, използващи хеш функции от влизане Boytsova [5] LM и се използва в режим на работа (в сравнение с разгледа ситуацията, че елементът не е в речника 3 и допустимата грешка, комплектът включва вход 20 заявки).
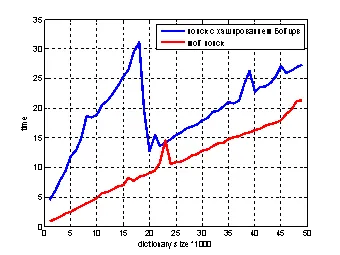
Фиг. 2 Сравнение на времеемко търсене с помощта на Boytsova функция и предложената статия
Въз основа на графиката, ние виждаме, че нашият метод показа най-добри резултати. Освен това, алгоритъмът се изпълнява в локална база данни и се използва успешно. Тя осигурява светкавична търсачката.
Основни понятия (генерирани автоматично). размита търсене, Левънстийн разстояние, алгоритъмът на размита търсене, алгоритъмът за търсене, в речника елементи Левънстийн метричен размер речник, проблемите на размита търсене, метода на размита извличане, сравнявайки думи, сравнявайки отнема много време, начин на индексиране на речника сравнението низ, множество метод речника елементи ускорение търсене, изграждането на компетентен търсене подмножество първоначалното речника, Разработване на размита алгоритъм, размит алгоритъм е оптимално, временни разходи за търсене.