Разпределение на Fischer (F-разпределение)

Помислете за разпределение на Фишер (F-разпределение). С funktsiiMSEXCELF.RASP () конструиране графики на разпределение и функцията на плътността вероятност, обясни използването на това разпределение на математическата статистика.

Определение. Ако U1 и U2 независими случайни променливи, които имат HI2 дистрибуция с k1 и k2stepenyami свобода съответно, разпределението на случайна променлива:

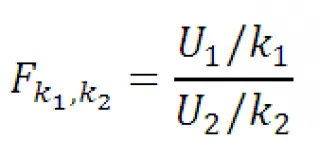
Тя се нарича F-разпределение с К1 параметри и k2.

PlotnostF разпределение изразен с формулата:

където F (...) - функцията гама:

ако алфа - положително цяло число, тогава е (а) = (а-1)!

Ето един пример на случайна променлива имащ F-разпределение.

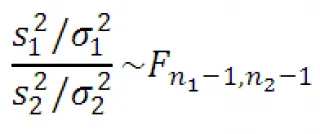
Той има F-разпределение. Това съотношение се нуждаем при тестване на хипотезата за равенство на отклонения от два нормално разпределение (F-тест).

графики на функции

F-разпределение с малък параметър (<50) имеет несимметричную форму, скошенную вправо (длинный правый хвост).

В файла върху листа от Пример Графиката показва графики на разпределение на плътността на вероятността и функция кумулативно разпределение.

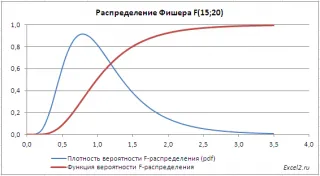
F-разпределение в MS EXCEL

Забележка: плътност на вероятност може да се изчисли директно с помощта на формулите (виж например файл.).

Примери за изчисления са дадени в пример файл на функции листа.

В MS EXCEL има и друга функция, която се използва за изчисляване F-Разпределение - това F.TEST (масив 1, array2). Тази функция връща резултата от F-теста. двустранен вероятност, че разликата между променливите на проби "array1" и "array2" е без значение. Предполага се, че пробата, направена от нормално разпределение.

Обратното функция F-разпределение

Обратното функция се използва за изчисляване на алфа квантил. т.е. за изчисляване на стойности за х даден вероятност алфа. където х трябва да отговарят на експресия P = алфа.

В MS EXCEL обратна функция се осъществява чрез използване на функция F.OBR ().

F.OBR.PH () функция се използва за изчисляване на горната квинтил. Т.е. Ако аргумент на функцията е определено ниво на значимост, например 0.05, функцията ще върне стойността на случайни променливи х, така че P (X> х) = 0,05. Като сравнение функция F.OBR на () връща стойност на случайни променливи х, така че P (X<=x)=0,05.

Горните функции могат да бъдат взаимозаменяеми, както Използват се следните формули върнат един и същ резултат:
F.OBR = (0,05; k1, k2)
F.OBR.PH = (1-0,05; k1, k2)
= FINV (1-0,05; k1, k2)