Проучването на линейни функции
Вашият браузър не поддържа вложени фреймове!
Функция е едно от водещите места в хода на учебната алгебра, и има множество приложения в други науки. В началото на изследването, да се мотивира, да интегрира Ви информираме, че не феномен, без процес в природата не може да бъде проучен, не машина може да бъде проектирано и след това да действа без пълно математическо описание. Един от инструментите за това е функция. Нейното проучване започва в 7-ми клас, като правило, децата не се ровя в определението. Особено концепции са трудни за достъп, като стойностите на домейни и обсег. Използване на известна връзката между стойностите в проблемите на движението, аз се измести цената на тяхната функция на езика, като държите връзка с неговата дефиниция. По този начин, концепцията на функция на учениците се формира на съзнателно ниво. В същото етап се извършва усърден труд на нови понятия: домейн, ценности домейни аргумент стойност на функцията. Използвайте предварително обучение: въвеждане на система за означаване D (където Y), E (Y), да се запознаят с концепцията за нула функция (аналитично и графично), при решаване на упражнения с части от постоянен знак. Колкото по-рано и по-студентите се срещат с трудни понятия, толкова по-добре те са наясно с нивото на дългосрочната памет. В изследването на линейната функция е препоръчително да се покаже връзката с решаването на линейни уравнения и системи, а по-късно с решение на линейни неравенства и техните системи. По време на лекцията, студентите получават голям блок (модул) на нова информация, така че в края на лекционния материал е "натиснат" и изготви резюме, че студентите трябва да знаят. Практически умения практикували по време на упражненията, които използват различни методи, които се основават индивидуална и самостоятелна работа.
1. Част от информацията на линейната функция.
Линейна функция е много често в практиката. дължина прът е линейна функция на температурата. Дължината на релсите, мост е линейна функция на температурата. Разстоянието, изминато от пешеходеца, влак, моторно превозно средство с постоянна скорост, - линейна функция на времето за пътуване.
Linear функция описва редица физически закони и зависимости. Помислете за някои от тях.
1) L = ето (1 + в) - линейно разширение на твърди вещества.
2) V = во (1 + БТ) - обемно разширение на твърди вещества.
3) р = Po (1 + в) - зависимостта на съпротивлението на температурата твърди проводници.
4) V = во + при - скорост равномерно ускорено движение.
5) х = Хо + VT - координата на равномерно движение.
Задача 1. Определете линейна функция на таблична информация:

Конструиране получава двойка (х; у) на координатната равнина и свързването им към всяка функция отделно (взехме стойността на х в една, ако намаляването стъпка, точките подреждат често, и ако стъпката е близо до нула, тогава точките ще се слеят в непрекъсната линия ), ние се отбележи, че точките се подреждат в права линия, в случай, че 1) и 2 случая). Поради факта, че функциите са избрани произволно (структура само графики у = 0,5x - 4, у = х + 5), можем да заключим, че графиката е права линейна функция. Използването на пряка собственост, която минава през две точки само една права линия е достатъчно за изграждане на директна вземе две точки.
6.Iz геометрията е известно, че линиите могат или да се припокриват или да са успоредни. Ние разглеждаме относителното положение на графиките на няколко функции.
1) Y = -x + 5, у = -x + 3, у = -x - 4; 2) Y = 2х + 2, у = х + 2, у = -0,5x + 2.
Ние изграждане на група от графики 1) и 2) и да се направят изводи.

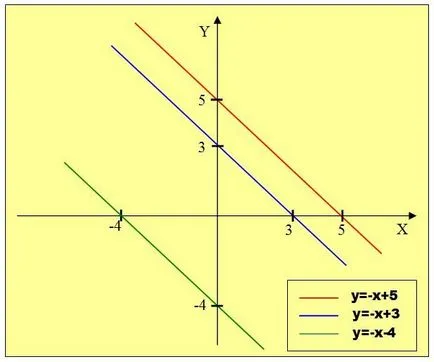
Графики функции 1), поставени паралелно, разглеждане на формулата, ние се отбележи, че всички функции имат еднакви коефициенти на х.
Функции графики 2) се пресичат в една точка (0, 2). Изследване на формула, ние се отбележи, че различни съотношения, и брой б = 2.
Освен това, не е трудно да се види, че линиите, определени от линейни функции с к> 0 форма с положителна посока Ox - остър ъгъл с к <0 тъп ъгъл. Поради това, коефициентът К се нарича склон.
7. Помислете за конкретните случаи на линейни функции в зависимост от коефициентите.
1) Ако б = 0, тогава функцията се форма у = KX, след което к = Y / х (съотношението показва колко време различен или каква част от Y на х).
Функция на форма Y = KX на, наречен пряко пропорционална. Тази функция има всички качества на линейна функция, неговата функция е. че когато х = 0, у = 0. директен графика пропорционалност минава през точката на произход (0, 0).
2) Когато к = 0, тогава функцията под формата у = б, т.е., за всяка стойност на х, функцията се същата стойност.
Функция на форма у = б, наречена постоянна. Графиката на функцията е права линия, минаваща през точка (0; б), успоредна на оста ОХ на графика В = 0 постоянна функция съвпада с оста х.
1. Определяне на функциите на формата Y = KX + б, където к, б - някои числа х -argument, Y- стойност на функцията се нарича линейна функция.
Графиката на линейна функция е права линия, минаваща през точка (0, Ь).
2. Ако б = 0, тогава функцията се форма у = KX на, наречен директна пропорционалност. директен графика пропорционалност минава през произхода.
3. Ако к = 0, функцията под формата у = б, се нарича константа. функция График преминава през точката (0; б), успоредно на оста на абсцисата.
4. Относителните положения на графиките на линейни функции.
Ако k1 = k2. графиките са успоредни;
Ако k1 и k2 не са равни, графиките се пресичат.
5. Примери на линейни функции графики см. По-горе.