Проучването на функции и графики - studopediya
Пълен изследователски функции за изграждане на своята програма включва следните елементи (не задължително в този ред).
1) Област на дефиницията на функцията (OOF) и домен на неговите стойности (OZF).
Ако домейнът на функцията не е специално определено, се счита, че той съвпада с границите на приемливите стойности на довод, т.е. множеството от всички точки х. за които операцията е възможно е. При намиране употреба OOF Уф елементарни функции. , , и др.
Обхват на функцията е само в случаите, когато това може да се отбележи веднага, въз основа на свойствата на елементарните функции, например, за функцията. очевидно.
2) Parity функция на честотата.
За да се установи паритет (странно) функция. като симетрична област определяне проверка на валидността уравнения () за всички OOF.
В случай на равенство на функция проучване на неговото поведение и графики може да се извърши само. и след това завърши графиката с помощта на симетрия на: за още функция симетричен по отношение на графика OY ос. и за странно - за произхода.
За да се установи периодичността на проверка на валидността на половете за OOF, където T се определя от формата на функцията. При изследването на периодичната функция извършва за един интервал периодичност.
3) функция непрекъснатост, точки на прекъсване, вертикалната асимптота.
За определяне на непрекъснатостта на непрекъснатостта интервали функции може да използват основните елементарни функции. В точките "подозрителен" руптура (отделни точки извън Уф), непрекъсваемост на условия за изпълнение на проверка. Ако функцията е прекъсната при x0. opredelyut вида на прекъсване.
Ако функцията има безкраен прекъсване в някакъв момент x0. тогава права линия х = x0 е вертикален асимптота на графиката на функцията. Ако само едностранно граници в x0 - x0 + 0 или 0 е безкрайна, тогава асимптота се нарича едностранно.
Ако функцията не е дефинирана в цялата реална ос, е необходимо да се изчисли едностранна функция граници в точките, ограничаване пропуски OOF. Ако едностранно ограничение на функцията в точка а. OOF граничат разликата е безкрайна, тогава х = а е едностранни вертикална асимптота графични функции. Например, ако Уф :. тогава ще трябва да се намери; ако тази граница ще бъде безкраен, тогава х = а е едностранни вертикална асимптота графични функции.
4) пропуски монотонност и екстремумите.
За определяне на интервалите на монотонност функции може да използват достатъчен критерий за монотонност.
Достатъчен критерий за монотонността на диференцируеми функции:
ако х интервал Î(А. В) производно на постоянен знак, функцията поддържа монотонността в този интервал, а именно: ако. след това е (х) се увеличава, ако. след това е (х) намалява.
За да се установи най-екстремни точки на функции може да използват необходимите и достатъчни условия за съществуването на екстремум.
Необходимо условие за наличието на екстремни функции. ако непрекъсната функция има екстремум в x0. неговите производни, в този момент е равен на нула или не съществува.
Точки, принадлежащи OOF в което производно е нула или не съществува, се наричат критични точки на функцията на първото производно (точки "съмнителни в крайна стойност").
Първият знак за наличието на достатъчно крайност. ако деривативни промени подписват, а след това x0 точка е изключителна стойност и този максимум, ако се промени знамение от положителни към отрицателни, и това е минимумът, ако промените в знаците от минус до плюс в минаваща през критичната точка x0 (от ляво на дясно). Ако минаваща през критична точка x0 производно не променя знак, а след това x0 точка не е екстремни функции.
Вторият достатъчен критерий за наличието на екстремни. ако - два пъти диференцируема в x0 и. След това, ако. След това x0 - минималната точка и ако. След това x0 - максималната точка.
За да намерите най-екстремни точки на първите функции са критичните точки на първата производна. След това ги проверите при изпълнение на достатъчни условия за съществуването на екстремни функции.
5) интервалите на изпъкналост, вдлъбнатина и инфлексна точка на графиката.
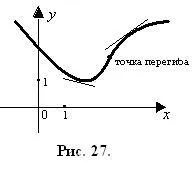
Точки, принадлежащи към кривата и разделя повдигнати части на вдлъбнатината, наречени инфлексните точки (фиг. 27).
Достатъчно условие за изпъкналост, вдлъбнатина на графиката на функцията: ако функцията е два пъти диференцируема и второто производно на постоянен знак за всички х Î(А; б), графиката на функцията е постоянна посока на изпъкналост в този интервал: от <0 – выпуклость вверх, при>0 - вдлъбнатина (изпъкналост надолу).
Необходимо условие за точка на инфлексия. ако x0 - абсцисата на инфлексната точка на графиката на функцията. след втората производна в този момент е равно на нула или не съществува.
Точки, принадлежащи към функцията за графика. които или не съществува, той се нарича критичните точки на функцията на своите втори деривати (точки "подозрителни за завой").
Достатъчно условие за точка на инфлексия. ако втората производна в минаваща през точка x0 на. подозрително да се огъват, знак на климата, на мястото на графиката с x0 абцисата е точка на инфлексия. Ако няма промени подписват при преминаване през x0. тогава не инфлексия.
При намиране на изпъкналостите интервали, вдлъбнатината на графиката на първата намерите най-критичните точки на втората производна, а след това съобщение интервали от постоянен знак на втората производна на Уф, ако. кривата е вдлъбната, като. кривата е изпъкнала. инфлексната точка се определя като се използва достатъчно условие на инфлексия.
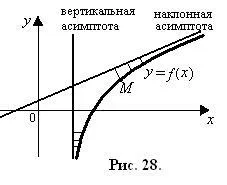
6) наклонена и хоризонтална асимптота.
Асимптота на кривата като безкраен клон се нарича права разстояние до която от текущата точка на кривата М клони към нула като точка М от произхода (фиг. 28).
Ако графиката има наклонена функция асимптота с уравнение. параметрите к и Б в уравнението на асимптота може да се намери чрез формулите:
Ако поне един от тези ограничения е безкрайна или не съществува, а след това на наклона на асимптотата там. В случая, където к = 0, графиката има хоризонтален асимптота с уравнение у = б.
В някои случаи (като правило, ако е (х) се изразява чрез експоненциална или логаритмична функция), графика може да има само асимптоти при или само.
Понякога графики клон в и имат различен асимптота.
7) точките на пресичане на графиката с координатните оси или друга допълнителна точка на графиката.
Допълнителни точки на графиката са в случаите, когато не е достатъчно информация, за да изберете размера на координатните оси, т.е. когато интервал OOF не крайни точки или инфлексните точки или пресечните точки на графиката с координатните оси.
Antiderivative и неопределен интеграл. интеграли на маса
(Х) функция F се нарича примитивна за F функция (X) в интервала (а. В), ако за всички X, равенството на този интервал
Неопределен интеграл на F функция (х) е набор от всички примитиви на функцията, т.е. неопределен неразделна - израз на формата. къде.
Процедурата за намиране на неопределен интеграл се нарича интеграция. В интегрирането използва: неразделна таблица (Таблица 2), свойствата на интеграли и специални методи на интеграция, основните от които - замяната на променлива и интеграция на части.
Таблица основни неопределени интеграли.
1 .; 2; 3; 4; 5; 6; 7; 8; 9;
10; 11; 12; 13; 14; 15; 16.