пролетен курс, теория и онлайн калкулатори

Под влияние на външни сили на организма са в състояние да придобият ускорението или деформира. Деформацията е промяната в размера и (или) на формата на тялото. Ако след премахване външно тяло натоварване възстановява нейната големина и форма напълно, то това деформация се нарича еластична.

Нека пролетта на фигура 1 сила на опън насочен вертикално надолу.

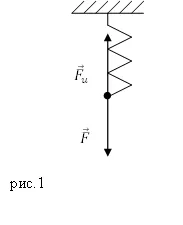
Когато са изложени на деформиране сила ($ \ Номера $) се увеличава дължината на пролетта. През пролетта има сила на еластичност ($> _ ф $), което балансира деформиране сила. Ако деформацията е малък и еластична, удължението на пружината ($ \ Delta л $) пропорционално на изкривяване на сила:

където като пропорционалността фактор актове извират постоянно $ к $. коефициент $ к $ The е известен също като коефициентът на еластичност, коефициент скованост. Твърдост (като свойство) характеризира еластичните свойства на тялото подлага на щам - е способността на тялото да се противопостави на външната сила, за да запази своите геометрични параметри. Коефициент на твърдост е основна характеристика на твърдост.

Коефициент на пролетта константа зависи от материала на строителството на пролетта, неговите геометрични характеристики. По този начин пружинната константа на спираловидна пружина, която се навива от тел с кръгло сечение, се деформира еластично по неговата ос се изчислява с помощта на формулата:

където $ G $ срязване модул (стойност зависи от материала); $ D $ - диаметър тел; $ D_p $ - диаметър на пружина; $ N $ - брой намотки.

Единици появят постоянни

Единицата за съотношение твърдост в Международната система единици (SI) е Нютон разделен на метър:

коефициент на твърдост е равна на силата, която трябва да се прилага на пружината за промяна на негов дължина на единица разстояние.

Коравината на съединения пружини

При свързване $ N $ коравина пружини съединение се изчислява като се използва формулата:

Ако пружините са свързани паралелно, полученият твърдостта е:

Примери за проблеми на твърдостта на пружините

Задача. Е потенциалната енергия ($ E_p $) системи деформация на две паралелни свързан пружините (2), ако те са равни скованост: $ k_1 = 1,000 \ \ Frac $; $ K_2 = 4,000 \ \ $ Фрак и удължението е $ \ Delta л = 0,01 $ m.

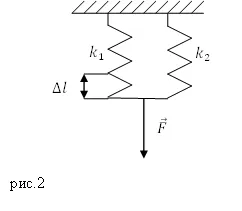
Решение. Успоредно връзка пролет система скованост изчислява като:

Потенциалната енергия на деформирана изчисли система с помощта на формулата:

Изчисляваме необходимата потенциалната енергия:

Решение. Направете чертеж.

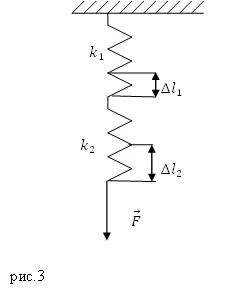
При свързване извори на всеки един от тях има един и същ деформираща сила ($ \ Номера $), като се използва този факт и закон на Хук откриваме първото разширение на пролетта:

\ [F = k_1 \ Delta l_1 = k_2 \ Delta l_2 \ да \ Delta l_1 = \ Frac \ лявата (2.1 \ дясно). \]

Работата на опън еластична сила на първия извор, е равна на:

Имайки предвид, получен в (2.1) Удължение първа пружина има:

Работата на втория еластичната сила:

Работна сила, която се простира на системата за пролетта като цяло, ще се намери като:

Заместването на дясната страна на изразите (2.3) и (2.4) в (2.5), ние получаваме: