правоъгълен триъгълник

Между другото, ако си спомняте добре какви краката и хипотенузата? Ако не, тогава погледнете на снимката - опресняване на знанията

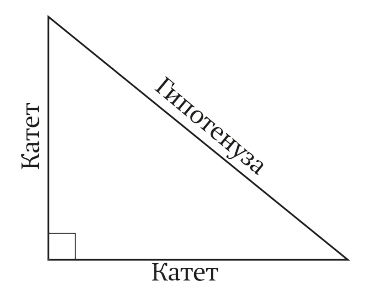
Възможно е, че многократно сте използвали Питагоровата теорема, но ако се зачуди защо такава теорема е вярно. Как ще го докаже? И нека да се процедира, както древните гърци. Равен квадрат със страна $ латекс а + б $.

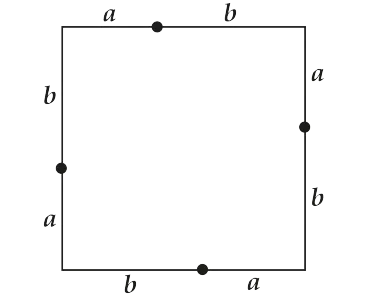
Вижте как умело сме разделили негова страна по дължината на сегмент $ латекс от $ и $ латекс б $!

И сега ние се присъединят към маркираните точки

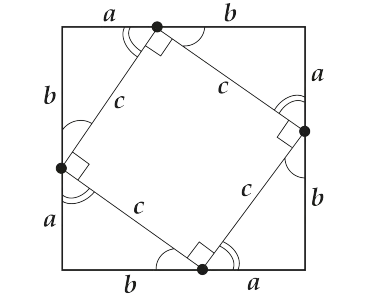
Каква е площта на по-големия квадрат? Точно така, $ латекс ^> $. По-малка площ? Разбира се, $ латекс в ^ 2 $. Имаше общата площ на четирите ъгъла. Представете си, че ние ги два взе и се облегна на един друг хипотенуза. Какво се случи? Два правоъгълника. Така че, района на "скрап" е $ латекс \ displaystyle 2ab $.

Сега нека да се съберат всички заедно.

Така че ние посетихме Питагор - доказа своята теорема древен начин.

Правоъгълен триъгълник тригонометрията и

Следващите отношения имат за правоъгълен триъгълник:

I. $ латекс \ displaystyle \ грях \ ъгъл А = \ Frac; \ \ грях \ ъгъл В = \ Frac \ $ \

Синуса на остър ъгъл равен на съотношението на другия крак на хипотенузата

II. $ Латекс \ displaystyle \ защото \ ъгъл А = \ Frac; \ \ \ защото \ ъгъл В = \ Frac $

Косинус на остър ъгъл равен на съотношението на хипотенузата към съседния крак.

III. $ Латекс \ displaystyle TG

\ Ъгъл А = \ Frac; \ \ ТГ

На допирателната на остър ъгъл равен на съотношението на другия крак към съседен крак.

IV. $ Латекс \ displaystyle CTG

\ Ъгъл А = \ Frac; \ \ CTG

Котангенс остър ъгъл равен на съотношението на съседни крака на обратен катет.

И отново всичко под формата на таблетки:

$ Латекс \ displaystyle \ грях \ ъгъл А = \ Фрак $

$ Латекс \ displaystyle \ грях \ ъгъл B = \ Фрак $

Ъгловата триъгълници са еднакви, ако един крак и под остър ъгъл на един триъгълник са равни на един крак и под остър ъгъл на друг триъгълник.

Внимание! Това е много важно, че краката са "подходящи". Например, ако това е така:

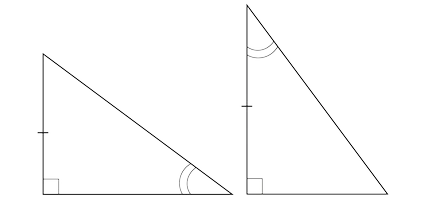
Това триъгълник не е прав. независимо от факта, че те имат един идентичен малък ъгъл.

Необходимо е, че и двете триъгълници крак е съседна, или и двете - противоположни.

Забелязахте ли разликите между знаците на равнопоставеността на правоъгълен триъгълник на обичайните признаци за равенство на триъгълници? Погледни в темата за "триъгълник" и обърна внимание на факта, че равенството на "обикновените" триъгълници нужда равенство на трите елемента: двете страни и ъгълът между тях, двата ъгъла и страната между две или три страни. Но за равенство на правоъгълен триъгълник достатъчно само два съответните елементи. Това е страхотно, нали?

Подобна е ситуацията и приликата с характеристиките на правоъгълни триъгълници.

Симптомите на правоъгълен триъгълник на сходство

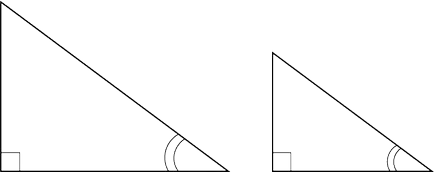
Ако правоъгълни триъгълници са на една и съща малък ъгъл. те са подобни.