Построяване на корен локус - studopediya
В повечето случаи, характеристика уравнението на системата учи да се изведе под формата
и където полиномите на комплексна променлива S. - параметър, който ще наречем променлива в бъдеще. (Този параметър може да бъде, например, трансфер коефициент к отворена система).
На траекториите, които описват корените на характеристика уравнение на равнина S при смяна на параметъра система от 0 до ∞ се наричат корен локус. Построяване корен локус ни позволяват да се изчисли ефекта върху стабилността и динамичните характеристики на промяната на системата в променлив параметър на.
С характеристика уравнение (1) с известни нули му съставни полиноми L (и) и D (и) може да бъде приблизително в равнина S строителство корен локус.
За тази цел (1) е пренаписана като:
Като се има предвид, че е - комплексна променлива, (2) може да се запише като две уравнения: уравнението на аргументи
и уравнението на модулите
Представлява под формата на:
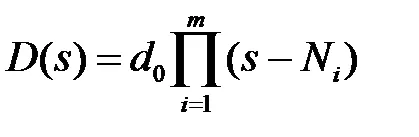
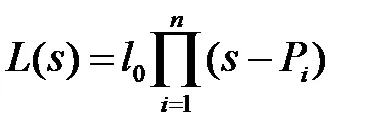
и където - коефициентът на най-високата степен S,
. - нули на полиноми и,
М и Н - поръчки и полиноми.
Аргументите уравнение (3) може да бъде пренаписана в следната форма:
От израза (5): S точка и равнина принадлежи на корен локус, ако сумата от аргумент вектор от нули
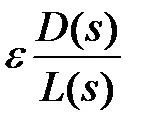
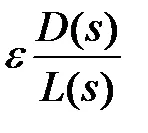
(По-горе е показано на Фигура 1)
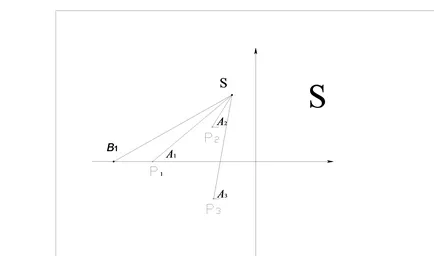
В тази цифра, определен от аргументите на векторите съставени от полюс
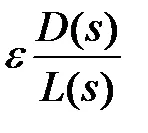
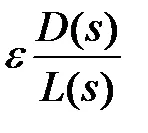
Въз основа на израза (5) можем да формулираме следните основни правила за изграждане на корен локус:
1. реално ос равнини S е ос на симетрия за корен локус за асимптоти на корен локус.
2. Когато се преминава от 0 до ∞ корен локус, идващи от полюсите
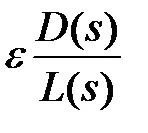
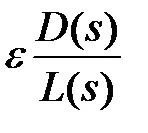
Ако п на брой полюси-голям от броя на нулите м, (М-М) клонове на корен локус ще отидат до безкрайност. Ако броят на нули надвишава броя на полюсите на (н-М) корен локус клонове идват от безкрайност.
3. Клоновете на главната локус, намиращи се в безкрайността са асимптотата. Броят на асимптоти равни. На асимптоти се пресичат в една точка в равнината на реалната ос S, където:
и да имат наклон ъгли по отношение на положителната посока на недвижими ос самолет S:
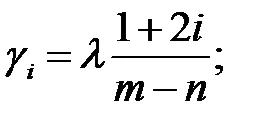
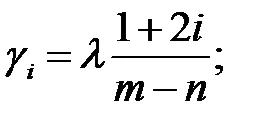
4. Точките на реалната S-ос вдясно от равнината, която е нечетен брой нули и полюси на
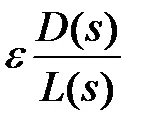
5. В определени точки на S равнина реалната ос принадлежащи корен локус, корен локус може изпълнени, разпръсне, един в горната част и друг в долната част на равнината S.
Посочени по-горе правила позволяват приблизително изпълняват заговор на корен локус.
Помислете за някои примери за изграждането на корен локус.
Построява се корен локус за променлив параметър к за затворена система, ако функцията за трансфер на системата за отворен цикъл:
Решение: характеристика уравнение на затворената система. Ние го представлява във формата. Това показва, че броят на нули е равно на 0, и на броя на полюсите е равно на 4. Тези стойности могат да бъдат получени чрез намиране на корените на знаменател. получавам

Нанесете полюсите в комплексната равнина. В съответствие с член 2 от всички корен локус трябва да отиде до безкрайност. Номер асимптота се равнява на 4-0 = 4. Определяне точка, разположена върху реалната ос, където се пресичат асимптоти -7,5
Ние определяме ъгли, които представляват асимптота с положителната посока на реалната ос (правило 3).
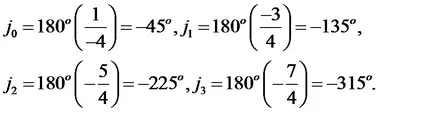
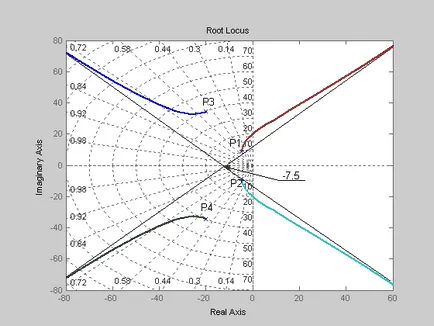
Нанесете асимптота на комплексната равнина, както е показано на фиг.2. Същата фигура показва корен локус, че излезе от полюсите и отидете до безкрайност, неограничени приближаващи изготвени асимптоти.
Решение: характеристика уравнението на затворената система има формата
Приравняването на нула на числителя и знаменателя, ние получаваме нули и полюси корен локус
Прилагане на полюсите и нули в комплекс равнина, както е показано на фигура 2. В съответствие с правило 1, два корен локус трябва да завършва на безкрайност, в допълнение, в съответствие с правило 4, няма смисъл не принадлежи на недвижими самолет корен локус.
В съответствие с правило 3, коренът локус две асимптоти, които се пресичат с реалната ос в точка
Ъглите между асимптоти и положителната посока на реалните ос са равни (обикновено 3)
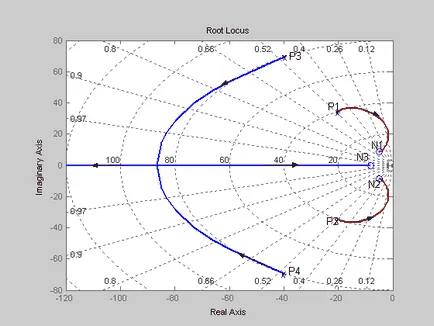
С това, че споменатият корен локус ще има формата, показана на фигура 3. Оставянето на корен локус на Р1 и Р2 полюси края в нули N1 и N2. Root Locus оставяйки P3 стълбове и P4 ще отидат до безкрайност за неопределено време приближава асимптоти пресичат реалната ос при -55.
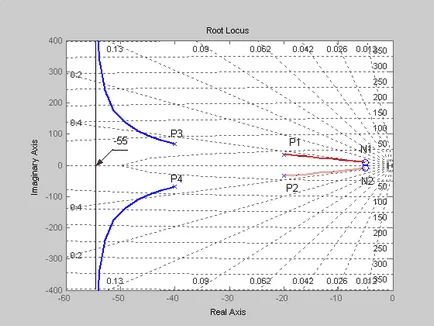
Решение: характеристика уравнение на затворената система
Ние го представлява във формата на
Нули корен локус са:
Първи корен локус са:
Ние прилагаме нули и полюси в комплексната равнина, както е показано на фиг. 4. В съответствие с правило 4, част от реалната ос, която се намира в ляво от нула N3 принадлежи корен локус, при което оста на този сегмент е асимптота за Hodograph изходящи до безкрайност.
Root място, конструирано в съответствие с горните правила са показани на същата фигура. Две корен локус, оставяйки полюсите Р1 и Р2 са нули за N1 и N2. Root локус, оставяйки полюсите P3 и P4 се събират в една точка на реалната ос на около 84, а след това единия край нула N3. а другият отива до безкрайност.