Построява кардиоидна предварително определен уравнение в полярни координати

Изграждане резултати сочат Mi (ρi; φi) в полярна координатна система и свързването им в гладка линия, получи достатъчно точно представяне на кардиоидна (фигура 4). ◄

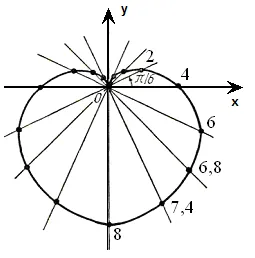
Изграждане на повърхността на данни и определяне на вида им (име):

а) Нека уравнението на каноничната форма

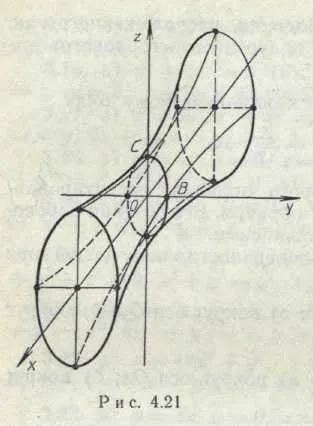
Ние получава уравнението на хиперболоидна, разположени както е показано на фиг. 5, semiaxes си "врата" елипса RH = / 2, OS = 2;

б) Нека уравнението на каноничната форма

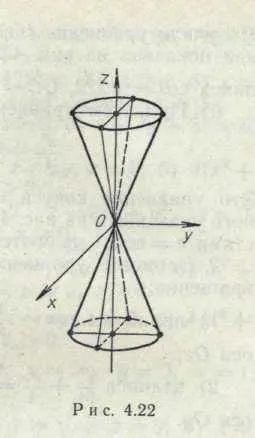
Този втори ред уравнение на конуса, ориентирани, както е показано на фиг. 6 начин. Неговата сечение равнини Z = конст са елипси. ◄

(Фиг. 5). Хиперболоидна (фиг. 6). Cone втори ред

Запишете уравнението на повърхността, получена от въртенето:

1) на параболата: а) около оста Oy; б) около оста Oz;

2) на елипсата: а) около ос Оз; б) около оста у.

►1. Като общо правило получаване уравнение повърхност въртене е:

(четвърти порядък алгебрични повърхности (Фигура 7).);

(Въртене параболоид (виж фиг. 8)).

Получен по Оз ос сплескана елипсоид на въртене (сфероид), неговите основни полуосите секции OA = OB = 8 OS = 2 (Фигура 9).

(Oy се простира по продължение на оста на въртене елипсоид (Фигура 10) :. OA = OC = 2, RH = 8). ◄

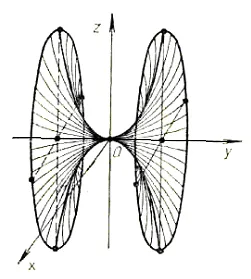
(Фиг. 7). Алгебрична повърхността на четвъртия ред

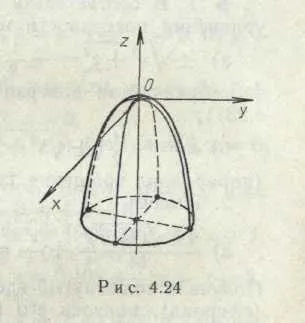
(Фиг. 8). параболоид на революция

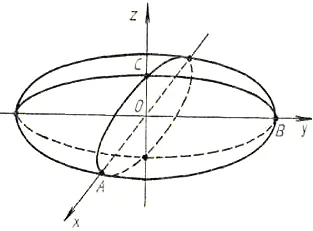
(Фиг. 9). елипсоид на въртене (сфероид) (сплескана по оста Оз)

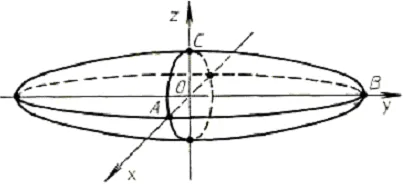
(Фиг. 10). елипсоид на въртене (удължаване по оста Oy)

Построява тяло ограничена от тези повърхности:

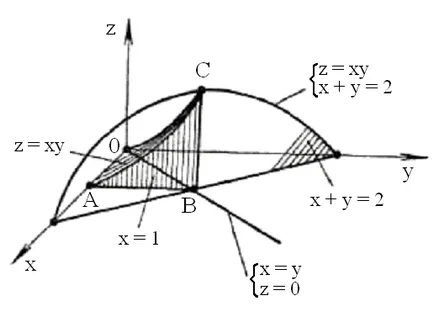
►a) Изграждане извършва на фиг. 11: OS - дъгата на парабола, който е точката на пресичане на хиперболична параболоид Z = XY с х = у равнина; дъга AC - пресичане на повърхност Z = XY равнина с х = 1; А (1, 0, 0), В (1, 1, 0), C (1, 1, 1) - характерната точка на тялото;

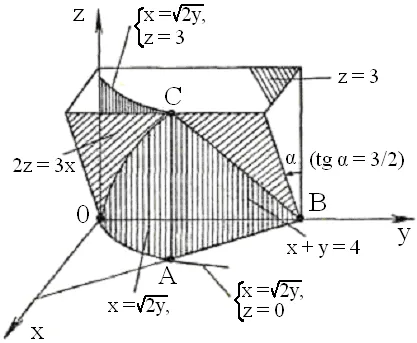
б) Конструиране извършва на фиг. 12: OS - дъгата на парабола, който е точката на пресичане на параболичен цилиндър равнина 2Z = 3x; А (2, 2, 0),

В (0, 4, 0), C (2; 2; 3), - характерната точка на тялото. ◄

2. Намерете определените граници.

детерминанта naytiminory и algebraicheskiedopolneniyaelementov AI2. това от елементите и-ти ред. 3; 7; -5), В (2, -4, 1). Задача 7 има предвид два вектора: = <8; 4; 1>, = <2;–2; 1>. Намери вектор. и копланарни вектори. перпендикулярна на вектора.

намери квадратна матрица) minorelementa; б) algebraicheskoedopolnenieelementa; в). Намерете) minorelementa; б) algebraicheskoedopolnenieelementa; в) детерминанта, от предшестващото нули в първия ред. Решение: а) Minoromelementa.

елемент матрица. " Определение. Algebraicheskimdopolneniemelementa aіk матрица се нарича Мала МИК тази матрица, умножена по (1) и + за: Algebraicheskoedopolnenieelementa. метод. Пример 1. Виж дадена матрица Det A. разтвор. Transform.

тата колона; наречен minoromelementa. След това, по дефиниция, счита (1) - algebraicheskoedopolnenieelementa. след това (2). Линейни операции с матрици задача. Намерете сбора на матрици и продукта. съвместим, той е длъжен да намери своето общо решение.

Този фактор се нарича minoromelementa Aij. Определени Мала - MIJ. Пример: За Naytiminorelementa детерминанта А12. на единица по-долу и Мала е: Algebraicheskimdopolneniemelementa детерминанта се нарича непълнолетен взела със себе си.