Получаването на синусоидално едн, електротехници

За д. г. а. синусоидална форма на вълната прилага алтернатор. Въпреки това, генераторът може да бъде заместен за изучаване принцип получаване синусоидална AC проводник под формата на правоъгълна рамка, която се върти по еднакъв магнитно поле с постоянна честота. (Фиг. 12.1).

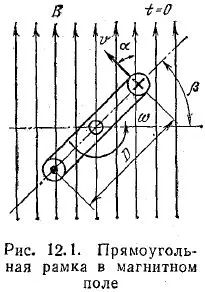
Въртенето на спиралата в постоянно магнитно поле

EMF в рамка с два активни дължина л диригент равна на:

(По-нататък, всички времеви различни количества :. токове, напрежения и др-едн ще бъдат означени с малки букви, за разлика от постоянни стойности за същите количества, които представляват главни букви).

С униформа въртене, линейната скорост на проводника не се променя:

и ъгъла между посоката на скоростта и посоката на магнитното поле варира линейно с времето:

Р на ъгъл определя позицията на въртящата се рама спрямо равнина, перпендикулярна на магнитната индукция. (Позиция конструкция по време на излитане т = 0 се характеризира с р ъгъл = 0) Следователно едн а. Рамкирани е синусоидална функция на времето

Най-голямата ценност е. г. а. Тя достига под ъгъл:

В горния случай, синусоидална вариант на напр. г. а. Това се постига чрез непрекъснато промяна на ъгъла, при който проводниците пресичат линии на магнитната индукция. Въпреки това, този метод за получаване напр. г. а. на практика тя не се прилага, защото е трудно да се създаде единна поле в достатъчно голям обем.

Получаване синусоидална едн в алтернатора

електрическия генератор генератори, промишлени тип AC синусоидална д. г. а. Оказва при постоянна ъгъл, но в нееднородно магнитно поле.

Магнитен генератор поле (радиално) във въздушната междина между статора и ротора е насочено радиално в периферията на ротора (фиг. 12.2, а). Магнитната индукция по въздушната междина се разпределя съгласно закон близо до синусоидална. Такова разпределение се постига чрез полюсните части на съответната форма. Синусоидална право разпределение на магнитната индукция по въздушната междина е показано на фиг. 12.2 б в разширена форма.

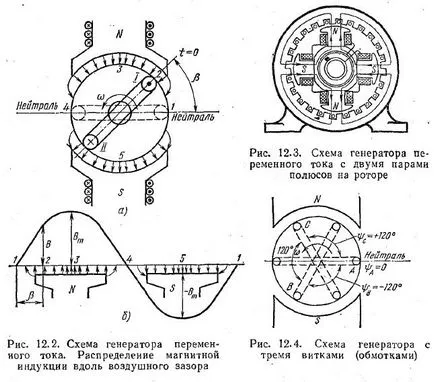
Във всяка точка на въздушната междина, позицията на който определя etsya ъгъл β, измерени от неутрален равнина (неутрален) обратно на часовниковата стрелка, магнитната индукция се изразява с уравнението

Неутралният равнина е перпендикулярна на оста поле и разделя магнитна система на симетрични части, едната от които се отнася до северния полюс, а другата - на юг.

Най-голямата стойност на магнитната индукция е в средата на пръта, т.е.. Е. В ъгли β = 90 ° (BM = В), и Р = 270 ° (В = -Bm). В неутрално (при β = 0 ° и β = 180 °) на магнитната индукция е нула (V = 0).

Фиг. 12.3 показва структурна схема на генератор на променлив ток с две двойки полюси, разположени върху ротора и винтови проводници, където се индуцира напр. г. а. поставени в слотовете на сърцевината на статора.

Забележка друг вариант алтернатори - генератор с три намотки (трифазен алтернатор), които във веригата на фиг. 12.4 представя три намотки на ротора. Равнини на рулони са под ъгъл от 120 ° помежду си.

Generator едн в ликвидация

С равномерно въртене на ротора в намотка (фигура 12.2, и -. А намотка) индуцира напр. г. а. определя по формулата

Заместването на експресията на магнитната индукция, получаваме

Когато β = 90 °, т. Е. В позиция долу център проводник прът, най-големият едн индуциран.

EMF уравнение може да се запише като:

Ние се получи същата зависимост на едн от време на време, както при завъртане на рамата (виж фигура 12.1 ..) се приема, че първоначалната позиция на бобината (т = 0), когато той съвпада с неутрална равнина:

По този начин, в този случай, е. г. а. Това е синусоидална функция на времето (фиг. 12.5). Същият резултат се получава чрез завъртане на пръта и останалите стационарна проводниците.

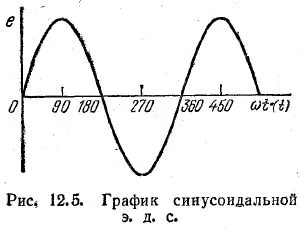
В правоъгълна координатна система, напр. г. а. могат да бъдат представени като функция на ъгъла β = ωt или функция на времето т. Зависимост д (ωt) и е (т) може да бъде представена чрез същия крива, но с различни мащаби на абсцисата, со различни във времето.

Токът в бобината на генератора

Ако генератор късо съединение намотка през съпротивлението, получено синусоидална токовата верига възниква повтарящ крива форма напр. г. а.

Ако приемем, устойчивост линейна верига равна на R, токът да се получи експресия:

където Im = Em / R- максимална стойност на тока.

Напрежение и ток синусоида може да се получава при използване на генератори, като не въртящи се части и магнитните полюси, например тръбни генератори.