Основните свойства на мощност серия - studopediya

1) всички точки лежат в интервала на конвергенция, количеството енергия серия е непрекъсната функция на променливата X:

2) Терминът мощност серия от термин може да се интегрира в интервала на сближаване:

3) Терминът захранващия серия от термина могат да се диференцират в интервал конвергенция:

Когато termwise интегриране и диференциране на степенния ред на интервали от конвергенция не се променят.

Пример 4. Виж сумата от серия

Решение. Първо намираме интервалът на конвергенция на серия N

Следователно, броят на интервал конвергенция (1, 1). Разграничаване (3.6), ние имаме

S ¢ (х) = 1 + х + х 2 +. + X п +.

Дясната страна на този израз - геометрична серия с р = х, която клони за ½x½<1. Поэтому, используя формулу суммы сходящейся геометрической прогрессии, получим

Следователно сумата от оригиналния сериал ще намерите интеграция

Намираме С от (5,6) следва, че S (0) = 0. Следователно

0 = - LN (1-0) + C, C = 0.

Следователно, S (х) = - LN (1-х) =.

Заедно с мощност серия по отношение на променливата х често се счита за променлива серия мощност (х-а), т.е. серия от формата

Очевидно този брой чрез заместване у = (х - а) се преобразува в поредица от типа (3.3). Ето защо, ако поредицата мощност (3.3) е интервалът на конвергенция - R

серия Тейлър. Да предположим, че F функция (х) при х = А има производни на всеки ред. Да предположим, че има редица сходни власт

a0 + A1 (х-а) + а2 (х-а) 2 +. AN + (х-а) п +. = (3.8)

чийто размер е равен на F функция (х). т.е.

Коефициентите на тази серия. Очевидно е, че е (а) = a0. Разнообразяване на (3.8) при х = а. имат А1 = F ¢ (а). Разнообразяване на (3.8) при х = двойна получи а2 = (е ¢¢ (а)) / 2. Продължавайки получаването на (3.8) може да се види, че редица фактори (са според формула

Мощност серия от формата

nazyvaetsyaryadom Taylor функция е (х).

В конкретния случай, а = 0 се прилага чрез серия Тейлър

и той се нарича серията Maclaurin.

Пример 5 в серия функция е Taylor (х) = е х.

Решение. Тъй като е х = (д х) ¢ = (д х) = ¢¢. (Е х) п. след това при х = 0 за е (х) = д х имат

F (0) = 1; е ¢ (0) = 1; е ¢¢ (0) = 1. ; е (п) (0) = 1.

Следователно, Maclaurin функция у = е х има формата

Серия (3.11) се съсредоточава върху цялата ос на функция у = е х.

Пример 6. разложи функция F Maclaurin (х) = sinx.

Решение. За F функция (х) = грях х, имаме: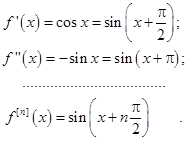

Следователно, серията Maclaurin за греха х:

По същия начин, ние получаваме разширяване на функционалните COS Х:

По същия начин, можете да получите разширяване серия Тейлър или Maklorenai много други функции.