Определяне на инерционния момент органи Overbeck махало
ОПРЕДЕЛЯНЕ инерционният момент на ОРГАНИ
ОТ Overbeck махало.
Цел - да се определи моментът на инерция на системата на четири еднакви маси m товари по два начина: 1) експериментално, използвайки Oberbeck махало 2) теоретично, това много съществени точки. Сравнете резултатите.
Инструменти и аксесоари. Overbeck махало, хронометър, мащабна линия, набор от стоки, шублер.
Момент на инерция - физическа величина, която характеризира въртене инерцията на движението на тялото.
Инерционният момент на материал, а оста на въртене е продукт на масата на точките на квадрата на разстоянието от оста (вж. Фиг. 1)
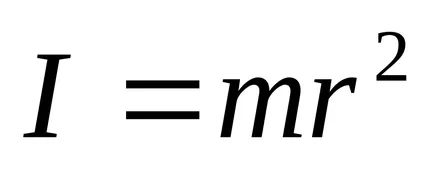

Инерционният момент спрямо произволна ос е сумата от моментите на инерцията на масови точки, които изграждат тялото, тази ос (вж. Фиг. 2)
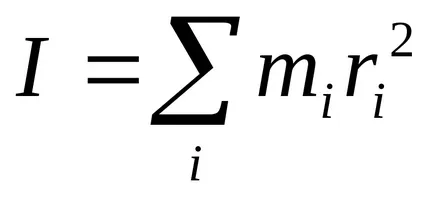
За хомогенни тела с правилна геометрична форма може да замени сумиране чрез интеграция.
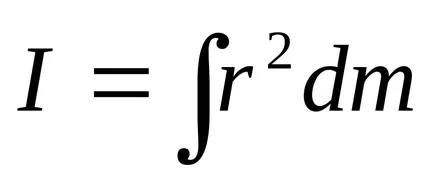
където дм = ρdV (ρ - вещества, плътност, DVD - елемент обем)
Така получени формула на някои органи тегло М по отношение на една ос, минаваща през центъра на тежестта:
а) дължината на пръта
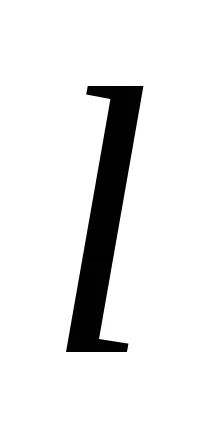
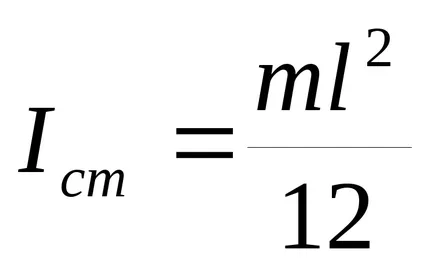
б) обръч (както и тънкостенни цилиндър) около ос, перпендикулярна на равнината на обръча и преминаваща през центъра на тежестта (която съвпада с оста на цилиндъра)
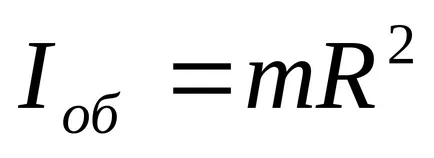
където
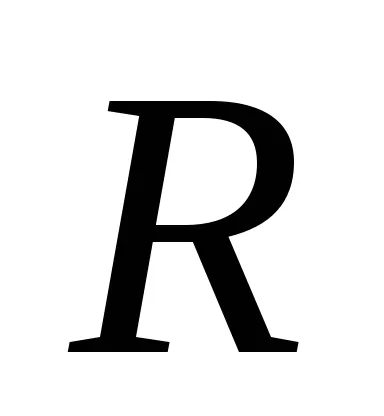
в) диск (твърд цилиндър) по отношение на една ос, перпендикулярна на диск равнина и преминаваща през центъра на тежестта (която съвпада с оста на цилиндъра)

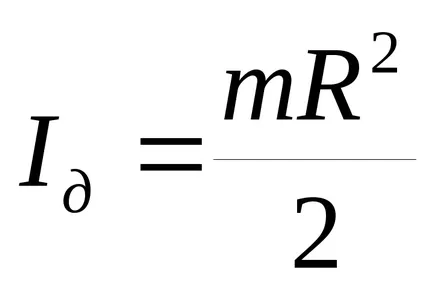
където
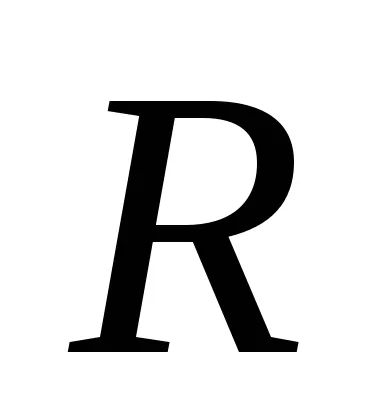
ж) сфера с радиус R около ос произволна посока, преминаваща през центъра на тежестта

Инерционният момент зависи от: 1) формата и размерите на тялото, 2) и масата разпределение, 3) от ос позиция по отношение на тялото.
теорема на Щайнер за успоредните оси изписва така:
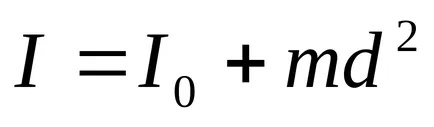
където
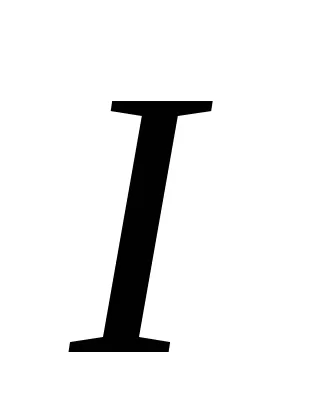
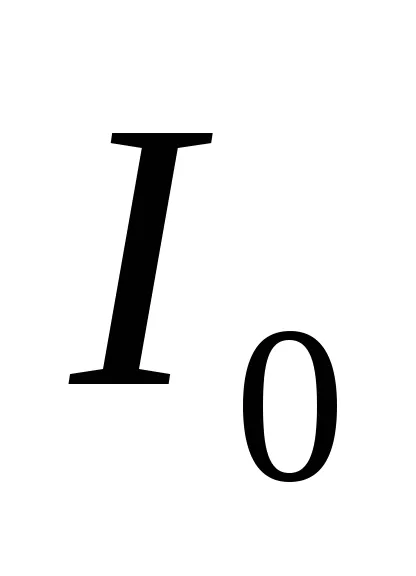

Овербек махалото е паяк, състояща се от ролка и четири равни пръти закрепен на хоризонталната ос (вж. Фигура 2). На пръчките на равни разстояния от оста на въртене
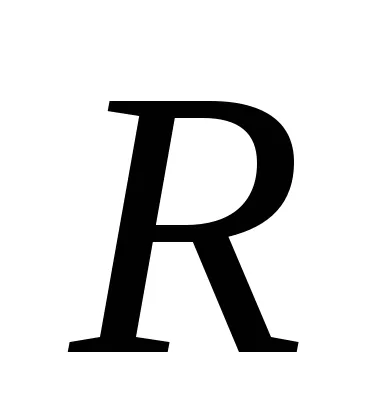
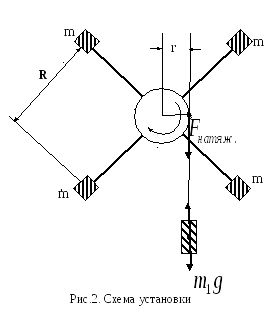
Пишем втория закон на Нютон за падане на товара в вектор форма

където
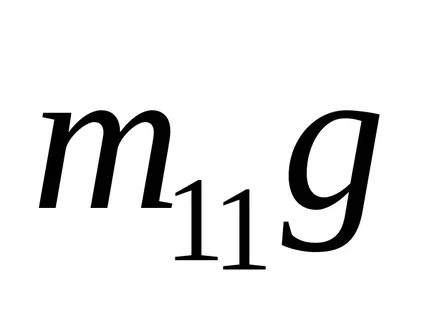
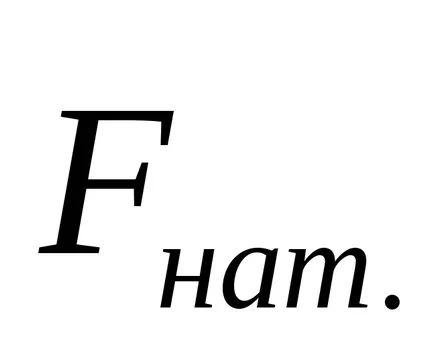

Като посоката на движение на товара е положителен, ние пренапише уравнение (I) в скаларна форма
какво ще се получи израз за силите на низ напрежение
Линейно ускорение на се определя по формулата на равномерно ускорена път движение без начална скорост
където H - височина на капка корабоплаването m1; т - време на падането.
Fnat сила опъване на конеца причинява бързото въртене на кръста. Основният закон на въртеливото движение на кръста, като се вземат предвид силите на триене може да се изписва така:
където M - в момента, в сила на затягане; Mtr - момент на триене; I - инерционен момент на кръста; I - ъглово ускорение, което се върти кръст. Големината на момента принуждава Mtr триене в сравнение със стойността на въртящия момент М е малък, и следователно могат да бъдат пренебрегвани.
От уравнение (5), дадена по-горе забележка окончателността получа-Ing формула за изчисляване на момента на инерция на кръста
където R - радиусът на шайбата. Ъглово ускорение се определя от формула I на
Заместването (3) и (7) в (6) се получи крайната формула за изчисляване на инерционния момент на жаба
Редът на изпълнение.
Опитно определяне на момента на инерция 4hgruzov.
1. Премахване от ядрата товар м.
2. рана в един слой на кордата на макарата, натоварването на настройка m1-солна предварително избрана височина Н. Освобождаване на напречната греда, измерва времето да се откажа товари Pomo-schyu хронометър. Опитът се повтаря пет пъти (на същата височина пада-ТА Н).
3. Затегнете краищата на пръти товари м.
4. Извършване на операция, посочена в параграф 2, хронометър за измерване на време, попадащи тон. Опитът да се повтаря пет пъти.
5. Използване на Vernier дебеломер, измерване на диаметъра на ролка г пет различни позиции.
6. Резултатите от измерването, записани в таблицата. Намери приблизителни стойности и студент метод оценява абсолютни стойности за допускане на грешки, т и г.
7. Съгласно формула (4), за да се изчисли стойността на линейно ускорение на, което намалява натоварването m1 в случаите:
б) база с много (а).
8. Съгласно формула (8), за да се изчисли инерционният момент на кръста без товар (Io) и товар (I), като се използват приблизителни стойности на m1, R, G, и полученият стойности А и ао.
Изчислете отклонението при измерване на следните формули:
Резултатите от измерванията и изчисленията
1. Теоретично намерите инерционният момент на системата зарежда маса 4 х т, на разстояние R от оста на въртене (приемайки товар материал точки)
2. Сравнение на резултатите от експеримента и изчисленията. Изваждане относителната грешка
и да се направи заключение за колко голяма е разликата в резултатите.
1. Какво се нарича инерционният момент на материалната точка и произволно тяло?
2. Какво определя инерционният момент на тяло спрямо оста на въртене?
3 предоставя примери на формули инерция органи. Как се получава?
4. Щайнер теорема за паралелни оси, както и неговото практическо приложение.
5. Заключение Формула за изчисляване на инерционния момент на кръста с и без товар.
1. Savelev И. В. Курс по обща физика: Обучение. помощ за технически колежи :. 3 тона Vol.1: Механика. Молекулна физика. - трето издание. Чл.-кор. - М. Наука, 1986 - 432s.
2. Detlaf А. А. Yavorsky BM Физика на курса: Обучение. помощ за технически колежи. - М. ВУ, 1989. - 607 стр. - парчета. указ. а. 588-603.
3. Зисман G. A. М. Тодес Обща физика курс за технически университета: 3 ТТ 1: Ръчно, Molecular физика, вълни - 4 изд .. стереотип. - М. Наука, 1974 - 340 стр.
4. Методически указания за лабораторни упражнения, под заглавие "Механика" .- Иваново, IHTI, 1989 (под редакцията на Birger BN).