Определяне на инерционен момент на цилиндъра и на коефициента на търкаляне триене, платформа съдържание

Lab N 6

Определяне на инерционен момент на цилиндъра

и коефициента на триене при търкаляне

Опитно определяне на момента на инерция на цилиндъра и сфера, сравнявайки инерционен момент получени експериментално и теоретично.

2. Теорията на въпрос

А. Инерционният момент на материал, а се определя от продукта от неговите мас и квадратен радиусът на въртене:

В различни точки на недвижими тялото са на различни разстояния от оста на въртене, така че всички инерционни моменти на масови точки са обобщени:

където дм - безкрайно малко маса на члена на твърдо тяло.

Тъй като m = Rv, където R -. Материя плътност, V - обем на тялото, тогава г т = R х DV, където DV - обем на частта от тяло.

Тогава формула (2) е под формата:

Като пример, помисли изходния въртящ момент на хомогенна диск на инерция около ос, перпендикулярна на равнината на диска и минаваща през центъра (фиг. 1).

Ние разделят диска в пръстеновидни DR слоеве с дебелина. Всички точки на един слой ще бъдат на същото разстояние от оста равна г.

Обемът на такъв слой е:

DV = а х 2prdr, където - дебелината на диска.

Диск хомогенна, R = конст.

Според уравнение (3) трябва:

Накрая, дискът въвеждане на тегло М, равно на R плътност на обема на диск р R2 на, ние получаваме:

Ако оста (0 ¢ ¢ 0), перпендикулярна на диска, но преминава през ръба (фиг. 1), моментът на инерция се определя с помощта на теоремата на Щайнер. теорема Щайнер е формулиран, както следва: инерционният момент J спрямо произволна ос е сумата от момента на инерция около ос, успоредна на това тяло и преминаваща през центъра на тежестта и продукт телесно тегло m квадрата на разстоянието D между осите:

По този начин, както и г = R, след това (7)

Ние се получи хомогенна сфера инерционни моменти около ос, минаваща през центъра му. За да се определи моментът на инерция на топката спрямо централната ос О тя се разделя на множество елементарни дискове (DH дебелина) XOU паралелна равнина (фиг. 2).

д ч = R г J = Rcos й г J, където R = Rcosj

начално диск маса с радиус R е равна на:

Инерционният момент елементарен радиус R диск дм и земята спрямо оста о е равно на:

Инерционен момент спрямо ос О получи чрез сумиране инерционни моменти на елементарните дискове и преминаване да се ограничи количеството на О до (за полукълбо).

За сфера инерционен момент е

След това обемът на сфера

Уравнение (12) определя момента на инерция на топката в (област), като се върти около центъра на масата. Ако топката се върти около ос, която не минава през центъра на масата, нейната инерционен момент се определя от теоремата на Щайнер (5).

Б. кинетичната енергия на тялото върти около фиксирана ос с ъглово skorostyuw равно

Ако тялото се върти, да се движи напред, (равнина на движение), нейната кинетична енергия е равна на сумата от кинетичната енергия на транслацията и ротационни движения:

Определяне на инерционния момент на топката е направено в тази работа по отношение на времето на подвижния топката с наклонена плоскост (фиг. 3).

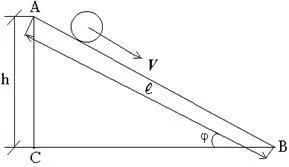
На върха на наклонената плоскост А кинетичната енергия на топката е равна на нула, потенциална енергия е MGH. В най-ниската точка (B) на наклонената плоскост на потенциалната енергия на топката е равна на нула, кинетичната енергия на

В допълнение, част от енергията отива да работи срещу силите на триене

А = m мг л cosj (15)

където m - коефициент на триене, L - дължина на наклонената равнина, J - ъгъла на основата на наклонената равнина. Т. к., Този ъгъл е малък, тогава грешка не надвишава 5% може да се счита cosj = I, след това

Според закона за запазване на енергията

При липсата на приплъзване ъгловата скорост, свързан с линейна връзка: w =, където R - радиус на въртене (радиус на сферата, цилиндър).

W Заместването в (17) и се редуцира до m, ние получаваме:

Ние изрази скоростта в края на наклонената равнина през време Т, и дължина L:

Формула (18) е под формата:

Следователно, от момента на инерция, равна на:

Формула (20) се изчислява за момента на инерция на цилиндъра и сфера.

Б. подвижен триене

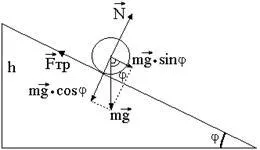
Цилиндър (топка) подвижен надолу по наклонената равнина под действието на три сили: силите на триене и наклонената равнина на реакцията (Фигура 4). Реакцията в съответствие с третия закон на Нютон е равна на абсолютната стойност на нормалната компонента на сила. с величина мг х Син.

Триенето между цилиндъра и наклонената повърхност се появява в точките на контакт. Тъй като тези цилиндрови точки за всяка точка от време са фиксирани (те образуват моментната ос на въртене), силата на триене е силата на триене (ролка) за почивка. Плъзгащи подвижния цилиндъра по равнина да липсва, при условие, че линейната скорост на контактните точки е равна на нула, което от своя страна се извършва, ако центъра на масата скорост е по всяко време на ъгловата скорост w на въртене на цилиндъра, умножена по радиуса на цилиндъра R

съответно, ускорение Аг центъра на инерция е равна на ъгловото ускорение умножена по радиуса:

При тези условия, силата на триене Tp не надвишава максималната стойност и цилиндър да се търкаля без приплъзване.

Пишем II-ти закон на Нютон за подвижен цилиндър (купа) с наклонената плоскост:

Триенето на въртящия момент по отношение на оста на цилиндъра е различна от нула и равно. След това, въз основа на закона за II-ри на динамиката на въртеливото движение на твърдо тяло може да се запише:

където J - инерционен момент на цилиндър спрямо нейната ос на въртене е равна.

Решаването на уравнение 21, 22, 23, ние откриваме, че

Известно е, че опитен право на търкаляне триене е:

където N - силата на нормално налягане, равно в нашия случай mgcosj,

R - радиус на цилиндър, m0 на - подвижен коефициент на триене.

С което се равнява на дясната страна на уравнения (24) и (25) получаваме:

Формула (26) се изчислява за цилиндъра.

За коефициента на триене при търкаляне топка получи независимо:

3. Описание на метода на монтаж и измерване

Инсталацията е наклонена равнина с улей, по която се движи топката. В горната част на топката в (цилиндър) се държи от електромагнит, най-ниската точка на коритото е краен изключвател, че се изключва таймера. Хронометърът се включва в U = 220V мрежа, заедно с електромагнит релейни ключове в мрежата - 24 V.

В зависимост от височината на наклонената равнина варира коефициента на триене, която се определя от формулите (26) и (27).

1. Задайте рампа до £ часа 15 см, измерване на височина ч.

2. Включване в контакт щепсел хронометъра и електромагнит.

3. Задайте диска за избор на "магнит".

4. Задайте топката (цилиндър) в горната част на канавката.

5. Включете диска за избор на "хронометър", ако топката (цилиндър) не се изключва таймера, повторете опит. Извадете време хронометър броене тон на движението на топката (цилиндър).

6. Параграфи 3-5 повторни 5 пъти.

7. изчисляване на средното време на търкаляне.

8. Поставете средно време във формулата (20). Намери пилот инерционен момент на топката (цилиндър).

10. изчислява абсолютната и относителната грешка от формулите:

цилиндър и сфера.

11. Изводът на работата.

Тестовите въпроси

1. Какво е посочена като въртеливо движение?

2. Какво се нарича момента на силите?

3. както е определено от момента на инерция на материална точка М по отношение на центъра на въртене, разположени на разстояние R?

4. От какво се определя от момента на инерция на тялото?

5. Напиши формула инерционен момент на цилиндъра, около една ос не, минаваща през центъра на въртене.

6. Напиши формула, която определя общата механична енергия на тялото, когато движението на самолет?

7. За някои формула определя инерционен момент на цилиндъра (купа) емпирично?

8. По някаква формула, определена инерционен момент на цилиндъра (купа) от теоретична?

9. Вземете формула за ускоряване на центъра на тежестта на топката със своя подвижен наклонената плоскост, с помощта на закона за запазване на енергията.

литература

1. Курсът по физика. В 3 m. Т. 1. механика. Молекулна физика. - М. Science, 1989.

2, и т.н. -. М. изпълнителния. седм. 1980

3. и т.н. -. М. образование, 1985.