Ограничения за използването на теста Дърбин-Уотсън

само ако следните условия могат да се прилагат тест за Дърбин-Уотсън:

Уравнението на регресия трябва да бъде свободен член на настоящето.

Променливи не са случайни.

Уравнението на регресия не е изостава стойности на зависимата променлива.

4. Той се използва за откриване на автокорелацията само между остатъци регресия в последователни наблюдения. Например, ако, но като се използва теста за Durbin-Уотсън е в състояние да открие всяко автокорелация.

3. генерализирана Методът на най-малките квадрати за смекчаване и премахване на хетероскедастицитет автокорелация

а) хетероскедастичност смекчаване

Ако знаете, че причината (и, съответно, с формата на хетероскедастицитет), а след това да реши проблема, можете да използвате генерализирана метода на най-малките квадрати (OLS).

Ако приемем, че вариацията на регресия остатъците свързани с някакъв вид зависимост от променливата ZT

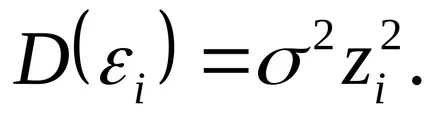
Както може да се променя:

1) стандартно отклонение σt (ако е известна), в този случай, метод на най-малките квадрати претеглят (WLS);

2) XI или

, т.е. otatkov вариацията пропорционална liboxi или .

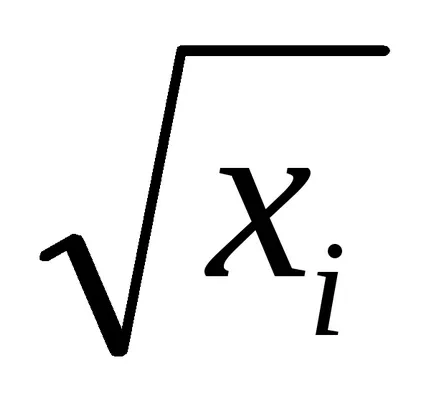
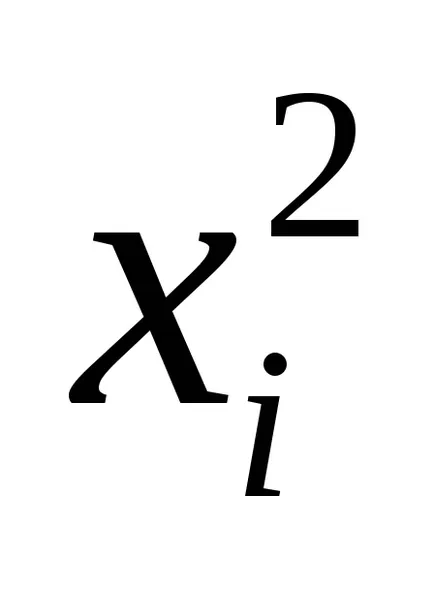
За да се отървете от хетероскедастицитет, разделете всяка дума на уравнението на регресия

(*)

където

случайна грешка.

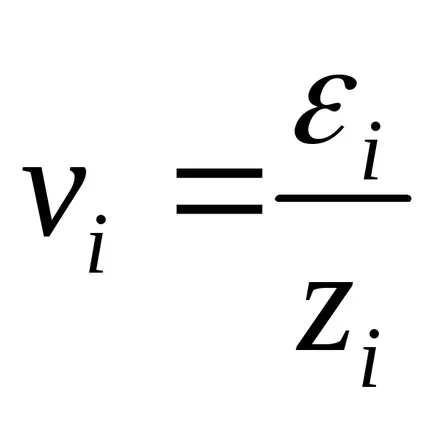
По този начин, уравнението на грешка (*) са homoscedasticity.

Въпреки това, на практика често не е възможно да се определи със сигурност причините и формите на хетероскедастичност. В този случай, можете да прехвърлите всички променливи в логаритмична форма (но трябва да се помни, че този метод не се прилага, ако променливите на модела могат да приемат нула или отрицателна стойност), или да се възползват от специални надеждни методи за оценка.

б) отстраняване на автокорелация

За да се премахне автокорелацията (както в случая на хетероскедастичност) могат да използват обща метода на най-малките квадрати (OLS).

Използването на AR (1) като модел на автокорелация, ние можем да напишете:

Ако приемем, че структурата на модела е константа, за период т -1 получи модел:

Размножава двете страни на уравнение (2), за да

;