Обратно пропорционалната функция алгебра

обратна функция пропорционалност - функция, определена от формула

където х - независима променлива, к - редица различни от нула.

Графиката на обратната пропорционалност е хипербола. Хипербола се състои от две части. (Така наречените две от графиката).

няколко точки, които трябва да знаете за изграждането на хипербола (повече точки - точният график). По-добре е да изберете тези, х, което е удобно да се разделят к.

Свойствата на обратни функции

1) Област на определяне на обратната състои от всички стойности на х, с изключение на нула:

2) Област на стойностите обратни - всички стойности на у, различни от нула:

3) Функцията обратна пропорционалност още няма нули.

хипербола клон се намира в координатните I и III тримесечия:

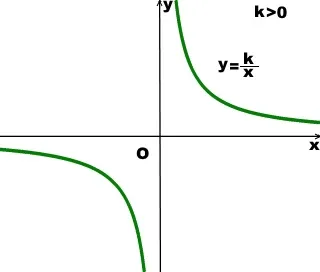
Намалява обратно пропорционална на всеки домен интервали, т.е. когато x∈ (-∞ 0) U (0; ∞).

Функция отнема положителна стойност, когато х> 0, или

Функцията се отрицателна стойност за х<0, или

хипербола клон, разположен во II и IV координира квартали:

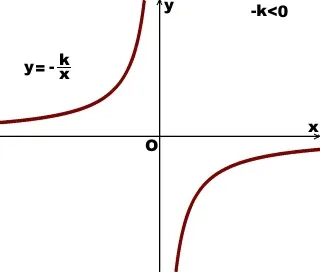
Връзка пропорционално увеличаване на всеки от периодите на домейна, т.е. под x∈ (-∞; 0) U (0; ∞).

Функция отнема положителна стойност, когато х<0, или

Функция отнема отрицателна стойност, когато х> 0, или

Ox и Oy ос е асимптота на обратната - насочва към която клонове на хиперболата за неопределено време приближаващи (но никога не постигат).

Следващия път, когато се вгледате в конкретни примери за това как да се изгради графика на обратна пропорционалност.