Обемът на правоъгълен паралелепипед е равно на 2,520 см (куб) и базова площ 168 см (квадрат

Дори не е необходимо изготвяне, тъй като той е решен на глас.

Така че, това, което е обема на кутията? Vpar Sosn = * H, където H е един от нашите ребра и всичко 4. Покажете на фигурата по-късно.

Така че ние открихме един ръб. Това остави другите двама, които се получават от техните бази.

Sosn = а * б; където а, Ь - базовата страна на паралелепипед.

Известно е, че а = б + 2

Така че вярно е:

Решението на квадратно уравнение, бързо и лесно.

Отговор: b1 = 12; b2 = -14 (не може да бъде толкова отрицателно)

Следователно, В = 12; а = 12 + 2 = 14

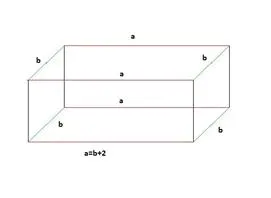
За яснота, I са специално определени ръб е червен цвят. Edge б в зелено, а височината Н на оставащото мастило.

Оказва се, че само с формата на паралелепипед 4 всяко ребро. Това е логично да се напише, че сумата ще бъде равен на:

Площта на основата на пирамидата е равна на 108 дм 2, а височината - 24 дм. Сглобяеми пирамида базова равнина, успоредна имат области 48 и 75 dm3. Намерете разстоянието между равнините на напречните сечения.

Така че ние имаме пирамида ABCS (боядисани триъгълна, защото в тази задача, няма разлика)

Също изготвят две секции DFE и D1F1E1 паралелна равнина ABC.

Сега ние виждаме, че ние получаваме подобна пирамида. Нека да разгледаме по реда на:

1) Пирамида Модулите ще бъде подобен на АВС на пирамидата. Според правило области сходство S (# 916; ABC) / S (# 916; DFE) = k2

След като установи, коефициент на сходство, можем да намерим височината на пирамидата Модулите.

108/48 = 2,25 → к = √ (2,25) = 1.5

Сега си спомням, че височината на стените имат сходни стойности по отношение на получаване на К = h1 / h2

Така че нашата височина е равна на 24 / ч (DfES) = 1,5 → ч (DfES) = 24 / 1.5 = 16

2) Също D1F1E1S пирамида подобен на ABCS. Нека да си височина, по същия начин.

24 / ч (D1F1E1S) = 1.2 → ч (D1F1E1S) = 24 / 1,2 = 20

3) Необходимо е разстоянието от самолета до DFE D1F1E1. Тя ще бъде равна на 20-16 = 4 дм.

В основата на пирамидата - равнобедрен триъгълник с ъгълът # 945; и радиуса на окръжност окръжност С. Двата неравни страничните повърхности перпендикулярно на основната равнина, и третата страна е склонен към нея под ъгъл # 946;. Откриване на страничната повърхност на пирамидата.

Фигурата показва пирамидални АВС, от върха S AVE Ведена Апотема SK към променливотоково в основата на равнобедрен триъгълник. Всичко това ние ще трябва да се реши този проблем.

Така че радиусът на описанието на кръг може да се намери на:

R = A / 2sin # 945; → CB = а = R * 2sin # 945;

Сега многозначителна страна CB намерите друга страна AC и AB, които са равни помежду си.

Нека да напишат какво области представляват страничната повърхност:

Сега трябва да се боя как да намерите всеки един от тях.

редовен триъгълна пирамида сегмент свързване на база с средната височина на Апотема на пирамида, m е еднаква височина с и образува пирамида, ъгълът # 946;. Намерете пълната повърхнина на пирамидата.

Картината показва пирамида ACBO, OM-височина, ОК-Апотема.

Mid точка L Апотема ОК, LM образува ъгъл с височина OM # 946;.

# 916; ОМК правоъгълна следователно ML е медианата на триъгълника, след OL = LM = LK = m

# 916; Olm равнобедрен следователно ∠OML = ∠LOM, което означава, че формите на ъгъл с Апотема височина # 946; (Показани).

Sbok = р • A / 2; където р - semiperimeter база, - Апотема OK.

В основата на нашата пирамида е правоъгълен триъгълник, чиито страни са равни. Нека да намерите на страната на базата, за това ние използваме вече наличните данни. Както е известно МК е радиусът на вписан в основния кръг.

R = AB * √ (3) / 6 → AB = 6R / √ (3)

Ние ще намерим това, което е R, знаейки, че грях # 946; = MK / OK → OK = MK / грях # 946; = 2 m / грях # 946;