Нова страница 1

2. бройни системи

"Всичко е число", - каза питагорейците подчертава изключително важната роля на номера на практика. Има много начини да представляват числа. Във всеки случай, броят представя със символа или група от символи (думи) от азбука. Ние наричаме тези символи на цифри. Да представлява номера, използвани nonpositional и позиционна бройна система.

системи Брой се делят на следните типове:

1. Устройството за система (система маркер);

2. nonpositional (код) на системата;

3. Позицията на системата.

1. системата за единен номер

Веднага след като хората започнаха да вярват, че имат нужда от писане на цифри. Археологическите находки в първобитните хора показват, че първоначално броя на елементите, показани на равно количество всякакви значки (тагове): стеснения, тирета, точки.

По-късно, с цел улесняване на сметката, иконите са групирани в три или пет. Такава система се нарича номера единица (единично) запис, тъй като всеки брой в него се образува чрез повтаряне едномарка символизираща единица. Ехото на единна система брой намерени днес. Така че, за да разберете какво година студент кадет, ще трябва да се преброи колко ленти пришити ръкава си. Без да го осъзнават, системата за идентификационен номер, използван от бебета, сочейки към пръстите на неговата възраст, и брои пръчки, използвани за обучение на студентите от клас 1 сметка на.

Една единствена система - не най-удобният начин да се напише номера. За да запишете като голяма част от досаден, и да направи запис в същото време може да бъде много дълъг. С всеки друг, по-удобен, системата брой с течение на времето.

2. nepozitsionnyh корен

Египетски система брой десетични nepozitsionnyh. Около третия хилядолетие преди Христа, древните египтяни са изобретили числова система, в която да посочи ключови номера 1, 10, 100 и т.н. използваните специални икони - знаци.

Всички други числа са съставени от тези ключови чрез операцията за допълнение. Древен Египет е десетична бройна система, но nonpositional.

В nepozitsionnyh брой системи количествен еквивалент на всяка цифра не зависят от позицията (позиция пространство) в броя на входната.

Например, за да представляват три рисунка 3252 лотос (три хиляди) две палмово сгънат лист (двеста), пет дъги (пет десетки) и две полюс (две единици). Големината на броя не зависи от реда, в който компонентите се намират героите си: те могат да горят от горе до долу, от дясно на ляво или променливо.

Римската бройна система. Nonpositional пример за система, която оцелява и до днес, може да служи като система за номериране, който е бил използван за повече от две години и половина преди хиляди години в древен Рим. В основата на римската корен са признаци на I (един пръст) за номер 1, V (отворена ръка) за номер 5, X (две сгънати дланите) до 10, както и да посочи номера 100, 500 и 1000 започва да се прилага от първите букви, съответстващи на латинската дума (C entum - сто, Demimille - половин хиляди, M Ille - хиляди).

За да запишете номера на римляните бе разлагат в размер на хиляда и петстотин, сто, като половината тип пчелна пита, десетки петата единици. Например десетичното число 28 е представен, както следва:

XXVIII = 10 + 10 + 5 + 1 + 1 + 1 (три десет, пет, три единици).

За цифрите за запис на междинните Римляни използва не само допълнение, но изваждане. В този случай, се прилагат следните правила. всеки малък знак поставен върху правото на по-голям се добавя към стойността си, а всяка по-малка марка сложи в ляво на толкова по-голям е извадена от него.

Например, IX - представлява 9, XI - означава 11.

Десетичен номер 28 е представен, както следва:

и десетичен номер 99 е тук, е една идея:

Римски цифри, използвани за дълго време. Преди 200 години на броя на търговски книжа са обозначени с римски цифри (се е смятало, че обичайните арабските цифри са лесни за фалшив). Римската бройна система сега се използва предимно за имена на важни дати, обеми, раздели и глави в книги.

Азбучен система номер. Още системи перфектен nepozitsionnyh цифри бяха азбучен система. Тези означения лекувани гръцки, славянски, финикийски и др. Те са числа от 1 до 9, цялото количество десетки (10 до 90) и цялото количество на сто (100-900), определен от букви от азбуката.

В древна Гърция азбучни обозначаване номера 1, 2. 9 означава първите девет букви от гръцката азбука, например = 1, б = 2, г = 3 и т.н. 9 следните букви (I = 10, к = 20, L = 30, m = 0 4 и т.н.), 10, 20. 90 се използва за обозначаване на цифрите и да определи номера 100, 200. 900 - 9 последните букви ( г = 100, S = 200, т = 300, и т.н.). Например, броят 141 е обозначен RMA.

В славянските народи на числените стойности на буквите в реда, установен азбука на славянски език, който се използва първия глаголицата и кирилицата и след това.

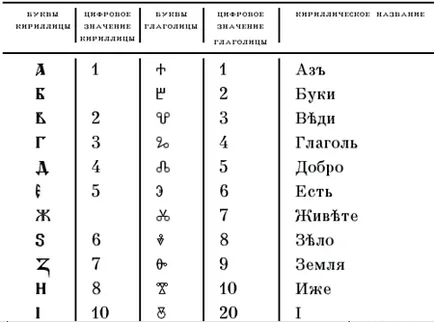
Старата руска азбука система номер

В България славянската номерация запазва до края на XVII век. При Петър I надделя така наречената арабска номерация, която ние използваме днес. Славянски номерация е запазена само в богослужебните книги.

Nonpositional системи с номера имат редица недостатъци:

1. Продължава да е налице необходимост от въвеждането на нови герои да пишат големи количества.

2. Не може да бъде дробни и отрицателни числа.

3. Трудно е да се изпълнява аритметични операции, тъй като няма изпълнение алгоритъм.

3. позиционно система номер

Основните предимства на всеки позиционен номер система - прости аритметични операции и ограничен брой знаци (цифри) се изисква, за да запишете всички номера.

База позиционна система за номериране се нарича мощност издигнат цяло число, което е равно на броя на цифрите, използвани за представянето номера в тази бройна система. Базата също показва колко пъти се променили количествената стойност на цифра като я преместите към следващата позиция.

Разнообразие от позиционни системи, както за корен може да се приема всяко число не по-малко от 2. Името на системата за номерация съответства на неговата основа (десетична, двоична, осмична, шестнадесетична, и така нататък. Г.).

В позиционни цифра системи еквивалентно количество (стойност) зависи от броя на своето място (позиция) в броя на входната.

Десетична система се характеризира с това, че 10 единици от единица освобождаване от отговорност да формират следващото маловажния бит. С други думи, различните бита представляват различни единици от 10 градуса.

В корен Q (Q-матрични нотация) битове единици са последователни сили на Q, с други думи, Q единици на единица освобождаване образуващи следващ етап. За записване номера в р-матрични нотация изисква различен брой р (0,1. Q-1).

В позиционна бройна система е всяко реално число в разширена форма може да бъде представен, както следва:

Тя е тази форма на писане на цифри, които използваме в ежедневието. В противен случай, сгъната форма на запис се нарича физическо или Цифров.

Пример 1. Десетична A10 = 4718,63 в разширена форма се изписва така:

А10 = 4 * 10 3 + 7 * 10 2 + 1 * 10 1 + 8 * 10 0 + 6 * 10 -1 + 3 * 10 -2

Пример 2. двоично число система.

В двоичен нотация база р = 2. В този случай, с формула (2.4) е под формата:

Тук аз - възможните цифри (0 и 1).

По този начин, двоично число е низ от нули и единици. В същото време тя има достатъчно голям брой битове. Бързото нарастване на броя на битовете - най-значимият недостатък на двоична система.

Задаване на двоично число А2 = 1001.1 ненагънати и провеждане изчисления, ние получаваме Това число, изразено в десетичната система:

Пример 3. осмично брой система.

Азбука: 0, 1, 2, 3, 4, 5, 6 и 7.

Определяне осмично брой A8 = 7764.1 ненагънати и провеждане изчисления, ние получаваме Това число, изразено в десетичната система:

A8 = 7 * 8 3 + 7 * 8 2 + 6 * 8 1 + 4 * 8 0 + 1 * 8 -1 = 3584 + 448 + 48 + 4 + 0,125 = 4084,12510

Пример 4. шестнадесетично число система.

Азбука: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е и F.

Има само десет от цифрите на шестнадесет са общо предназначение 0,1, ... 9. За да запишете останалите цифри (10, 11, 12, 13, 14 и 15), които обикновено се използват първите пет букви от латинската азбука.

По този начин, 3AF16 запис е:

3AF16 = 3 * 16 2 + 10 * 16 1 + 15 * 16 0 = 768 + 160 + 15 = 94310.

Пример 5. Пишем началото на естествените числа в десетичен и бинарни системи: