Нивото на цилиндричен съд с течност достига на каква височина ще остане ниво
В цилиндричен съд, нивото на течността да достигне до 16 см. На каква височина ще бъде в нивото на течността, ако му се излива във втората цилиндричен съд, чийто диаметър е 2 пъти по-голям от първия диаметър? Отговорът се изразява в сантиметри.
Обема на бутилката V = πR 2 часа.
В първия случай, течен обем, равен на V = 16πR 2.
Ако диаметърът на втория съд 2 пъти по-голям от диаметъра на първия съд, и радиусът на втория съд 2 пъти по-голям от радиуса на първия съд. Следователно, след кръвопреливане течността във втория съд, неговия обем може да бъде изчислен по формулата:
V = π (2R) 2 ч = 4πR 2 часа, където Н - височина желания.
Тъй като обемът на течността остава постоянно преливане, тези количества са:
16πR 2 = 4πR 2 часа,
Цилиндрите и конуси имат обща база и общата височина. Изчислява се обема на буталото, когато обемът на конуса е равен на 20.
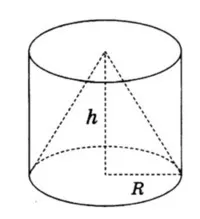
височина Cone равно на височината на радиуса на цилиндър и конус, равен на радиуса на цилиндъра (вж. фиг.).
Обемът на конуса е равна на VK = (1/3) πR 2 часа = 20.
Обемът на цилиндъра е СМТ = πR 2 3Vk = Н = 3 х 20 = 60.
Следователно, обемът на цилиндъра е 3 пъти по-голям от обема на конуса и е равна на 60.
Цилиндрите и конуси имат обща база и общата височина. Изчислява се обема на буталото, когато обемът на конуса е равен на 19.

височина Cone равно на височината на радиуса на цилиндър и конус, равен на радиуса на цилиндъра (вж. фиг.).
Обемът на конуса е равна на VK = (1/3) πR 2 часа = 19.
Обемът на цилиндъра е СМТ = πR 2 3Vk = Н = 3 * 19 = 57.
Следователно, обемът на цилиндъра е 3 пъти по-голям от обема на конуса и е равна на 57.
В редовното четириъгълна височината на пирамидата е равно на 2, на страничен ръб е 4. Намерете обема си.
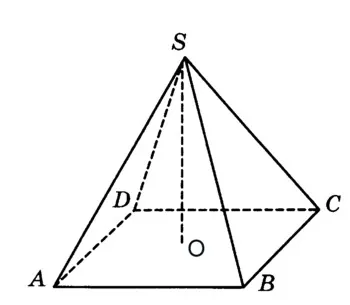
Обемът на пирамидата е равно на V = (1/3) H. Sosn
За H = SO = 2 състояние, SC = 4.
база редовен четириъгълна пирамида е квадрат. Ние намери своя път, т.е. намерят AB.
SOC на правоъгълен триъгълник от питагорова теорема, ние имаме:
SC 2 = SO 2 + 2 ° С
OC 2 = SC 2 - SO 2,
OC 2 2 = 4 - 2 = 2 12,
OC = √ (12) = 2√3,
AC = 4√3, AC 2 = 48.
От правоъгълния триъгълник ABC (имайки предвид, че AB = BC) от питагорова теорема, ние имаме:
2 AC = AB + BC 2 2 = 2АВ 2
48 = 2АВ 2. AB 2 = 24.
V = (1/3) * 24 * 2 = 16.
Цилиндрите и конуси имат обща база и общата височина. Изчислява се обема на буталото, когато обемът на конуса е равен на 12.

височина Cone равно на височината на радиуса на цилиндър и конус, равен на радиуса на цилиндъра (вж. фиг.).
Обемът на конуса е равна на VK = (1/3) πR 2 часа = 12.
Обемът на цилиндъра е СМТ = πR 2 3Vk = Н = 3 * 12 = 36.
Следователно, обемът на цилиндъра е 3 пъти по-голям от обема на конуса и е равна на 36.